1. はじめに

PHYSBOはCOMBOを元に開発されたベイズ最適化パッケージです。高速でスケーラブルなベイズ最適化を行うことができ、多くのデータ量を取り扱うことができるのが特徴です。PHYSBOはPythonライブラリなので、設定した最適化問題に適用できるようPHYSBOの機能を呼び出すPythonスクリプトを自分で作成する必要があります。

この記事では、PHYSBOのチュートリアルを参考に作成した、PHYSBOと第一原理計算ソフトウェアQuantum Espresso (QE)を使ったシリコンSi結晶の格子定数を最適化するPythonスクリプトを紹介します。(2019/10/8-10に開催された計算物質科学イノベーションキャンプでCOMBOを用いて作成したスクリプトをもとにしております。)格子定数などの結晶構造の最適化問題は、もっとも安定なエネルギー(最低エネルギー)である結晶構造を求めるという問題です。この構造最適化には、エネルギーの微分値を利用した勾配法を用いることが多いですが、勾配法は局所解にトラップされやすい問題があります。一方、与えられた範囲内での候補点(グリッド)を全て計算するグリッドサーチを用いれば局所解に留まることなく候補内での最適値を求められますが、グリッド数によっては計算量がかなり増えてしまいます。ベイズ最適化では、与えられた範囲内で計算すべき候補点を効率よく探索することができるので、グリッドサーチよりもずっと短時間で大域的な最適解を見つけられそうだと期待できます。

今回の記事では、PHYSBOがプレインストールされているMateriApps LIVE! ver. 3.3を使います。なお、使用するMateriApps LIVE!のバージョンが3.3より以前のものである場合は以下のコマンドを実行するとPHYSBOをインストールできます。

sudo apt-get update
sudo apt-get install physbo

2. 計算の準備

まず、physbo_qeという実行用ディレクトリを作り、そこに計算に使うインプットファイルとスクリプトをダウンロード&解凍しましょう。

mkdir physbo_qe
cd physbo_qe
wget https://ma.issp.u-tokyo.ac.jp/wp-content/uploads/sites/3/2021/05/physbo_qe.zip
unzip physbo_qe.zip

unzipで解凍すると、pythonスクリプトphysbo_qe.pyとQEのインプットファイルの雛形scf.in.orgがでてきます。この雛形ファイルはQEのレビュー記事で紹介した例題にあるインプットを少し変更したものになっています。

physbo_qe.pyでは

格子定数の候補点を決める。
格子定数が記載されていないscf.in.orgから、候補点から選んだ格子定数を追記したscf.inを作成する。
作成したscf.inを使ったQEの計算を行い、全エネルギーを求める。
ベイズ最適化に基づいて、全エネルギーが最小になる格子定数の次の候補点が提案される。
指定した最適化ステップ数までb.-d.を繰り返し、最後に結果を出力する。

といったことを行っています。a, d, eに関してはPHYSBOのチュートリアルをほぼそのまま使っていますが、bとcに関しては今回の最適化問題用に書き換えています。physbo_qe.pyの8行目には

exec_cmd = "OMP_NUM_THREADS=1 mpirun -np 4 pw.x < scf.in > scf.out"

とQEの実行時にしているコマンドが記載されています。サンプルでは、1スレッド4MPIプロセスの計算を行うよう設定されています。実行する前に、mousepadなどのテキストエディタを利用してご自身の環境に合った並列数に変更してください。

3. 計算の実行

まず、physbo_qe.pyの使い方を見てみましょう。

python3 physbo_qe.py -h

と打つと、次のような使い方が表示されます。

usage: qe_physbo.py [-h] [-r RANGELIST RANGELIST] [-g GRID] [-p PROBE]
[-i ITV]

Optimize lattice constant of Si using QE and Physbo

optional arguments:
-h, --help show this help message and exit
-r RANGELIST RANGELIST, --range RANGELIST RANGELIST
min, max (default:7.5, 15)
-g GRID, --grid GRID # of grid (default:101)
-p PROBE, --probe PROBE
max_num_probes for bayes opt (default:10)
-i ITV, --interval ITV
interval for bayes opt (default:0)

end

例えば-rを使うと、探索する格子定数(単位はBohr)の範囲を指定できます。オプションを指定しない場合は、デフォルト値が採用されます。

それでは実際に動かしてみましょう。

python3 physbo_qe.py -p 5 -i 0

を実行してみてください。これは、7.5~15Bohrの範囲(-rで指定。今回はデフォルト値。)を101分割(-gで指定。今回はデフォルト値。)した候補リストの中から、ガウス過程で用いられるハイパーパラメータの学習を始めだけ行い(-iで指定)、5回(-pで指定)のベイズ最適化により最適値を見つける、ということをしています。すると下図のような結果が表示されます。(図のwindowを閉じるとターミナルに戻れます。なお、図はoutput.pdfに出力されています。)

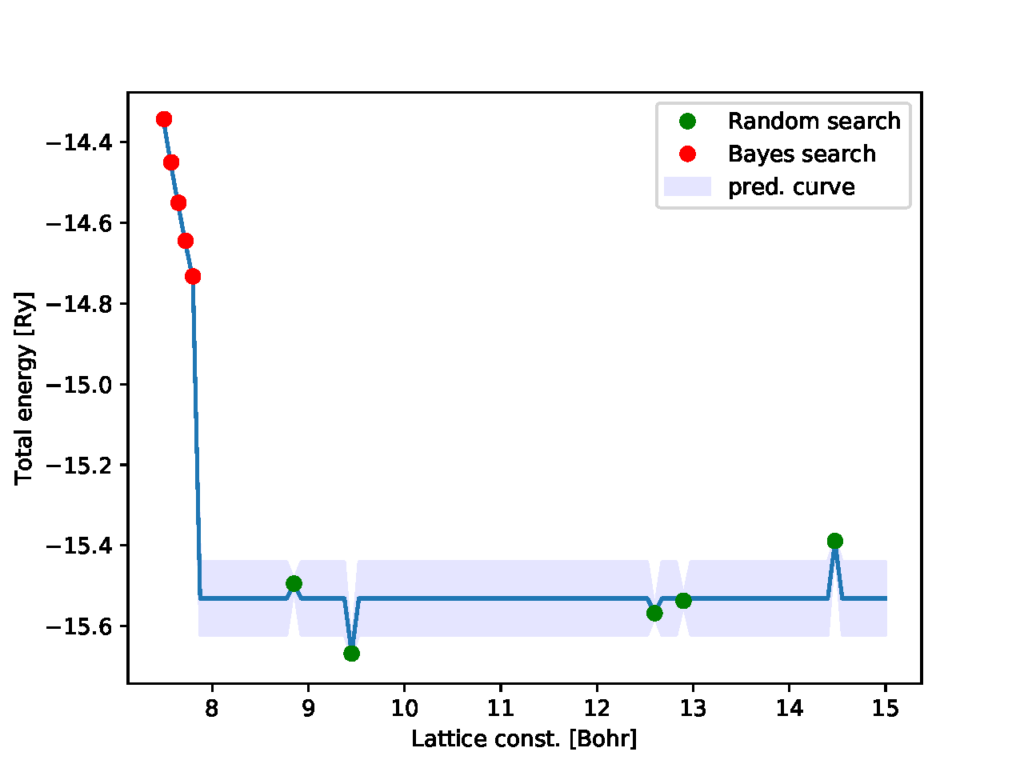
緑丸がベイズ最適化を行う前にランダムサーチ(今回のスクリプトでは5回)した結果、赤丸がベイズ最適化の結果、青線が最適化終了時の回帰曲線(ガウス過程の期待値と分散)です。青線は、緑丸のデータ点に基づいて学習されたハイパーパラメータをそのまま使った予測になっていますが、今回の予測はどんな格子定数でも同じような値を返すような回帰曲線になってしまいました。そのため、ベイズ最適化で選ばれる候補も候補リストの最小値から順番に試しているような結果になっています。

原因としては、ランダムサーチの結果により学習されたハイパーパラメータにあると考えられます。そのため、解消する方法として、ランダムサーチの結果を変える、もしくはハイパーパラメータの学習をベイズ最適化中にも行うようにすれば対処できそうです。乱数のシードを変えるのはスクリプトの76行目

policy.set_seed(0)

の0を違う値に変更してください。

今回は、もう一つの方法、ハイパーパラメータの学習をベイズ最適化中に行う、をやってみます。次のコマンドを実行してみてください。

python3 physbo_qe.py -p 10 -i 5

前回のものとの違いは、ベイズ最適化を10回(-pで指定)実行し、ガウス過程で用いられるハイパーパラメータの学習を5回ごとに行っている(-iで指定)点です。得られる結果は次のようになります。

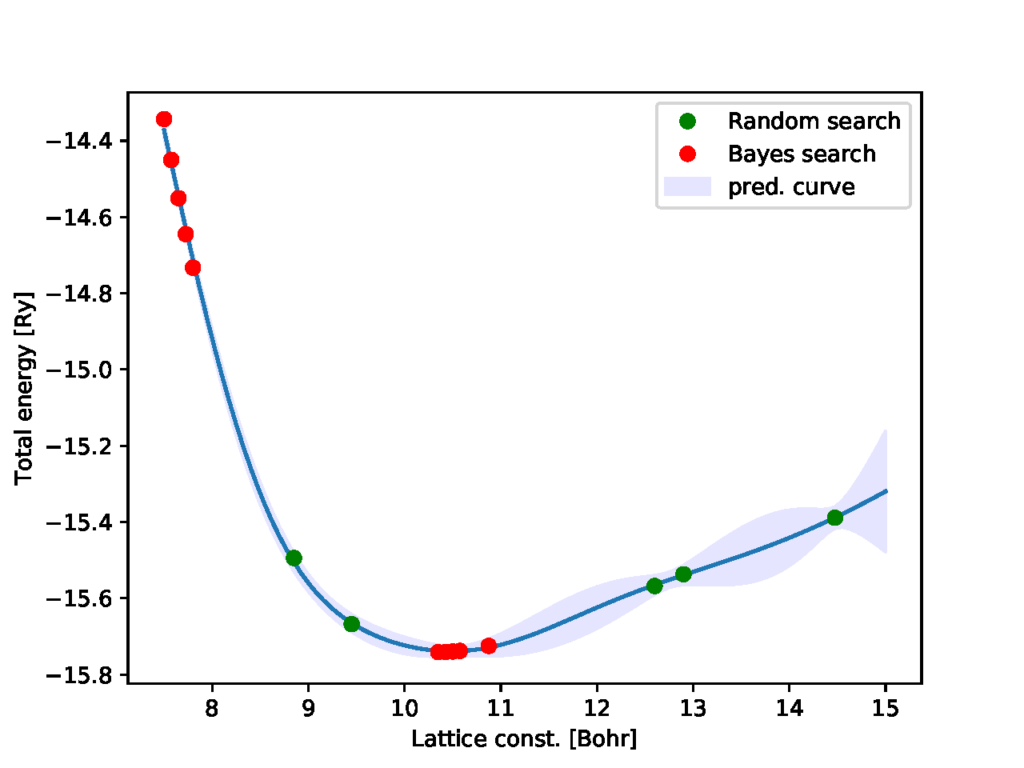
初めの5点は先ほどまでの結果と同じですが、ハイパーパラメータがこれまでの測定点を使って再学習されることにより予測線が改善されました。その結果として、ベイズ最適化の点も最適解付近で探索され始めています。ターミナルには格子定数の最適値とそのエネルギーが最後に出力されます。

best_fx: 15.74127496 Ry at 10.35 Bohr

今回の最適化した範囲では10.35 Bohrが最適値となることがわかりました。実験値が5.43Å~10.26Bohrなので大体一致しているように見えます。

4. まとめ

Physboを利用したSi結晶の格子定数最適化について紹介しました。今回は単純な1変数最適化問題への適用で、メッシュも100点ほどでしたが、Physboはより複雑な最適化問題へも適用できます。また、同種の結晶構造最適化・探索計算はCrySPyでも実行できるようです。今後はPhysboやCrySPYを用いて複雑な系での問題に挑戦してみたいと思います。

物質科学シミュレーションのポータルサイト

PHYSBO (optimization tools for PHYsics based on Bayesian Optimization )

Physboを使った結晶構造最適化
Last Update:2023/07/13

あなたはすでに投票済みです！

1. はじめに

2. 計算の準備

3. 計算の実行

4. まとめ