Xというフラストレート磁性体の磁化過程を計算したいのですが。

まず、理論計算を行なう際には、対象の物質を記述するハミルトニアン(ハイゼンベルグ模型など)を適切に設定する必要があります。通常は格子構造から推測できる相互作用を仮定して、理論計算と実験結果を比較してその妥当性を検証する方法が一般的ですので、ここではその方法について説明します。理論計算だけから物質の記述するハミルトニアンを得る方法(それが実行できるアプリとしては例えば、RESPACK など)も最近開発されていますが、ここでは詳述しません。

一般的なハミルトニアン(幾何学的フラストレーションを持つ場合など)に適用できる汎用的な計算手法は厳密対角化です。厳密対角化はサイズの制限は非常に大きいですが(通常のスパコンですとスピン1/2の系で30-40サイト程度が限界)、その範囲で厳密な計算が実行できるのが特徴です。

厳密対角化を行なうソフトウェアとしてはスピン1/2のハイゼンベルグ模型を取り扱えるTITPACK,スピン1の系を取り扱えるkobepack,ハイゼンベルグ模型・ハバード模型などを取り扱えるspinpack,任意の2体相互作用・1体ポテンシャルを持つハミルトニアンが取り扱えるHΦ, ALPS があります。ここではHΦを用いた磁化過程の計算結果について説明します。

HΦを使ってフラストレート磁性体の磁化過程の例として、二次元カゴメ格子(27サイト)の基底状態の磁化過程を計算する場合の流れを示します。次のようなインプットファイルを用意します(インプットファイルの詳細はHΦのマニュアルをみてください。)。

a0W = 3
a0L = 0
a1W = 0
a1L = 3
J = 1
model = spin
lattice = kagome
method = CG
2Sz = 1

ここで2Szが磁化の大きさに対応していて、これを変えた計算を
行っていくことで基底状態の磁化過程を得ることができます。
計算を行うサンプルスクリプトはgithub においてあります。
結果は例えば、以下の図のようになります(縦軸は磁化m,横軸は磁場hです)。

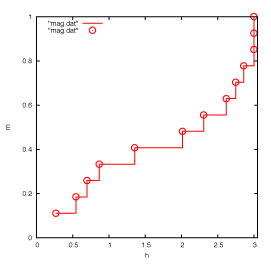
この計算結果と実験結果をくらべることで、どれくらい理想のカゴメ格子に近いかを判定できます。
また、次近接の交換相互作用などの相互作用を入れることができますので、
その磁化過程と比較することで、現実の物質を記述するハミルトニアンを推定することができます。