MateriApps
物質科学シミュレーションのポータルサイト

現在アプリ掲載数328件

お問合せ / アプリ掲載依頼
もっと詳しく探す

ALAMODE

  • 公開度：3 ★★★
  • ドキュメント充実度：2 ★★☆

格子振動の非調和性を露わに考慮した原子間ポテンシャルを構築するプログラムパッケージ。VASPやQuantum ESPRESSOなどの第一原理計算プログラムやLAMMPSの計算結果から調和・非調和force constantを推定し、それらをもとにフォノン分散、フォノン状態密度、グリューナイゼン定数、フォノン‐フォノン散乱強度、格子熱伝導率、有限温度における非調和フォノン、フォノン由来の自由エネルギーなどを計算することが可能。

ALAMODEとQuantum ESPRESSOを用いたSiの熱伝導度の計算
Last Update:2024/10/04
あなたはすでに投票済みです！

MateriApps開発チーム

１．はじめに

本レビューではDocker版のMateriApps LIVE!を利用して、ALAMODEとQuantum ESPRESSOを用いたSiのフォノンのバンド図・状態密度と熱伝導度の計算方法を解説します。Docker版のMateriApps LIVE!のインストール方法および使い方はここを参照してください。すでにDocker版MateriApps LIVE!にALAMODEはインストールされていますが、一部のツールが正しく動作しないので、Docker版のMateriApps LIVE!を立ち上げたら、最新のALAMODEにアップグレードしておきます。

sudo apt-get update
sudo apt-get install alamode

２．電子状態計算

まずQuantum ESPRESSOを用いて、2x2x2のスーパセルを考えてSiの電子状態計算を行っておきます。Dockerにログインできたら、新しくディレクトリを作成して、そのディレクトリに入っておきます。

mkdir alamode
cd alamode

次にMateriApps LIVE!に入っているALAMODEのサンプルファイルをコピーしてきます。

cp /usr/share/alamode/example/Si/reference/si222.pw.in .

次にsi222.pw.inを編集しておきます。例えばemacsを用いる場合は、

emacs si222.pw.in &

とします。ファイルの修正点は以下の通りです。

１．&CONTROLセクション中の pseudo_dir = ‘/home/tadano/etc/pseudo/’, を pseudo_dir = ‘./’, に変更する

修正したらセーブしておきましょう（以下、編集方法については同様なので省略します）。修正後のファイルは以下のようになります。

&CONTROL
  calculation = 'scf',
  restart_mode = 'from_scratch' ,
  outdir = './',
  pseudo_dir = './',
  prefix = 'si' ,
  tprnfor = .true. ,
  tstress = .true.
/
&SYSTEM
  ibrav = 1,
  celldm(1)  = 20.406,
  nat = 64,
  ntyp = 1,
  ecutwfc = 40 ,
  ecutrho = 320 ,
  occupations = 'smearing',
  smearing = 'gauss',
  degauss = 0.001,
/
&ELECTRONS
  diagonalization = 'david' ,
  electron_maxstep= 1000,
  conv_thr= 5.0d-11
/
ATOMIC_SPECIES
   Si   28.0855  Si.pz-n-kjpaw_psl.0.1.UPF
K_POINTS automatic
 4 4 4 1 1 1
ATOMIC_POSITIONS  crystal
Si 0.000000000000000 0.000000000000000 0.000000000000000
Si 0.000000000000000 0.000000000000000 0.500000000000000
Si 0.000000000000000 0.250000000000000 0.250000000000000
(中略)
Si 0.875000000000000 0.625000000000000 0.875000000000000
Si 0.875000000000000 0.875000000000000 0.125000000000000
Si 0.875000000000000 0.875000000000000 0.625000000000000

次に擬ポテンシャルファイル(Si.pz-n-kjpaw_psl.0.1.UPF)をここからダウンロードしておきます。Docker版のMateriApps LIVE!では事前にshareフォルダを作成しておくとファイル共有が可能ですので、Docker内ではなく普通にPCでダウンロードして、shareフォルダで渡しておくといいでしょう。この擬ポテンシャルファイルはさきほど作成したalamodeディレクトリに移動させておきます。

最後に電子状態計算を実行します。1CPUでの計算の場合は、

pw.x < si222.pw.in > si222.pw.out

並列計算が可能な場合は

mpirun -np (並列数) pw.x < si222.pw.in > si222.pw.out

とします。並列版のほうが速く終わるので、並列計算環境のあるクラスター計算機で実行するのがよいでしょう。どちらのコマンドも最後に「 &」をつけると、バックグラウンドで実行してくれるようになります(以下の計算の実行も同様なので、以下では1CPUの実行方法のみ記述します)。この計算は10分程度で終わるはずです。IEEE_UNDERFLOW_FLAGの例外発生などの警告が表示されるかもしれませんが、以下の計算に影響はありません。

３．ALAMODEの実行

次にALAMODEを実行してみましょう。フォノンに関係する量を求めるために下準備をしておきます。まず原子間力定数の計算をします。サンプルから入力ファイルをコピーしておきます。

cp /usr/share/alamode/example/Si/si_alm.in .
cp si_alm.in si222.harmonic.in

次にsi222.harmonic.inを編集します。変更点は以下の通りです。

１．&general中でMODE = suggest とする

２．&optimizeセクションを削除

修正後のファイルは以下のようになります。

&general
  PREFIX = si222
  MODE = suggest
  NAT = 64; NKD = 1
  KD = Si
/
&interaction
  NORDER = 1  # 1: harmonic, 2: cubic, ..
/
&cell
  20.406 # factor in Bohr unit
  1.0 0.0 0.0 # a1
  0.0 1.0 0.0 # a2
  0.0 0.0 1.0 # a3
/
&cutoff 
  Si-Si None
/
&position
  1 0.0000000000000000 0.0000000000000000 0.0000000000000000   
  1 0.0000000000000000 0.0000000000000000 0.5000000000000000
  (中略)
  1 0.8750000000000000 0.8750000000000000 0.1250000000000000
  1 0.8750000000000000 0.8750000000000000 0.6250000000000000
/

ALAMODEのプログラムであるALMを実行します。

alm si222.harmonic.in > si222.harmonic.log

実行が正常に終了すれば、si222.pattern_HARMONIC というファイルができます。さらにALAMODEに付属のPythonスクリプトを使ってQEの入力ファイルを作成します。

python3 /usr/share/alamode/tools/displace.py --QE si222.pw.in --mag 0.01 --prefix disp -pf si222.pattern_HARMONIC

実行が正常に終了すれば、Quantum ESPRESSOの入力ファイルが1つだけ(disp1.pw.in)生成されます。出てきた入力ファイルをQuantum ESPRESSOで実行します:

pw.x < disp1.pw.in > disp1.pw.out

スーパーセルを用いているので、この計算は時間がかかります(数時間程度)。disp1.pw.outに各原子に働く力の情報が含まれているので、これをALAMODEに付属しているPythonスクリプトで抽出します。

python3 /usr/share/alamode/tools/extract.py --QE si222.pw.in *.pw.out > DFSET_harmonic

最後にALMを用いて原子間力定数を計算します。すでに今のディレクトリにあるsi_alm.inをコピーして、ALM用の入力ファイルを作成します。

cp si_alm.in si222.harmonic_opt.in

si222.harmonic_opt.inを編集します。変更点は以下の通りです。

１．&optimizeセクションでDFSET = DFSET_harmonicとする

&general
  PREFIX = si222
  MODE = opt
  NAT = 64; NKD = 1
  KD = Si
/
&optimize
 DFSET = DFSET_harmonic
/
&interaction
  NORDER = 1  # 1: harmonic, 2: cubic, ..
/
&cell
  20.406 # factor in Bohr unit
  1.0 0.0 0.0 # a1
  0.0 1.0 0.0 # a2
  0.0 0.0 1.0 # a3
/
&cutoff 
  Si-Si None
/
&position
  1 0.0000000000000000 0.0000000000000000 0.0000000000000000   
  1 0.0000000000000000 0.0000000000000000 0.5000000000000000
  (中略)
  1 0.8750000000000000 0.8750000000000000 0.1250000000000000
  1 0.8750000000000000 0.8750000000000000 0.6250000000000000
/

編集が終わったらALMを実行します。

alm si222.harmonic_opt.in > si222.harmonic_opt.log

si222.fcs と si222.xml の二つのファイルが生成されたら成功です。これらのファイルに原子間力定数が出力されています。

４．フォノンのバンド図

次に求めた原子間力定数を用いて、フォノンのバンド図を描いてみます。ALAMODEに用意されている入力ファイルをコピーします。

cp /usr/share/alamode/example/Si/si_phband.in .

次にANPHONを実行します。

anphon si_phband.in > si_phband.log

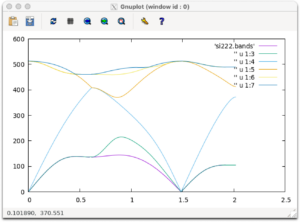
si222.bandsが生成されていたら成功です。gnuplotを使ってグラフをかいてみましょう。

gnuplot
plot 'si222.bands' w l,'' u 1:3 w l,'' u 1:4 w l,'' u 1:5 w l,'' u 1:6 w l,'' u 1:7 w l

以下のようなグラフが出力されれば成功です。

gnuplotから抜けるには

exit

とします。

５．フォノンの状態密度

今度はフォノンの状態密度を求めてみましょう。さきほどフォノンのバンド図を描くのに用いた入力ファイルをコピーして、新しい入力ファイルを準備します。

cp si_phband.in si_phdos.in

次にsi_phdos.inを編集します。修正点は以下のとおりです。

１．&generalフィールドでDELTA_E=1を追加

２．&kpointフィールドを以下のように変更

&kpoint
  2
  40 40 40
/

ANPHONを用いて状態密度を計算します。

anphon si_phdos.in > si_phdos.log

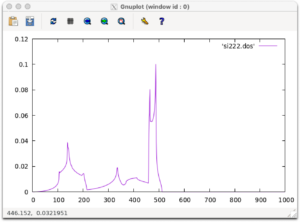
状態密度の結果はsi222.dosに出力されます。gnuplotでグラフにしてみましょう。

gnuplot
plot 'si222.dos' w l

以下のような図が出力されれば成功です。

６．３次の原子間力定数の計算

次にフォノンの非線形に関わる量を計算していきます。入力ファイルを用意します。

cp si222.harmonic.in si222.cubic.in

si_222.cubic.inを以下のように修正しておきます。

１．&generalセクションで PREFIX = si222_cubic　とする

２．&interactionで NORDER = 2 とする

３．&cutoff で Si-Si None 7.3 とする

入力ファイルは以下のようになります。

&general
  PREFIX = si222_cubic
  MODE = suggest
  NAT = 64; NKD = 1
  KD = Si
/
&interaction
  NORDER = 2  # 1: harmonic, 2: cubic, ..
/
&cell
  20.406 # factor in Bohr unit
  1.0 0.0 0.0 # a1
  0.0 1.0 0.0 # a2
  0.0 0.0 1.0 # a3
/
&cutoff 
  Si-Si None 7.3
/
&position
  1 0.0000000000000000 0.0000000000000000 0.0000000000000000   
  1 0.0000000000000000 0.0000000000000000 0.5000000000000000
  (中略)
  1 0.8750000000000000 0.8750000000000000 0.1250000000000000
  1 0.8750000000000000 0.8750000000000000 0.6250000000000000
/

次にALMを実行します。

alm si222.cubic.in > si222.cubic.log

si222_cubic.pattern_HARMONIC と si222_cubic.pattern_ANHARM3 の2つのファイルができます。 si222_cubic.pattern_HARMONIC は調和項の原子間力を求めるときに使った si222.pattern_HARMONIC と同一です。

ALAMODEに付属するツールによって、原子位置を少しずらした配置の電子状態を計算するquantum ESPRESSOの入力ファイルを生成します。

python3 /usr/share/alamode/tools/displace.py --QE si222.pw.in --mag 0.01 --prefix disp -pf si222_cubic.pattern_ANHARM3

これにより、disp01.pw.in から disp20.pw.in までの20個の入力ファイルが生成されます。この入力ファイルをすべて用いて、Quantum ESPRESSOを実行します。(とても時間がかかります。本当に実行する場合は性能のよいクラスター計算機を利用してください。またPCで本チュートリアルを実行している人は、後述の説明も参照してください。)

mpirun -np 4 pw.x < disp01.pw.in > disp01.pw.out
mpirun -np 4 pw.x < disp02.pw.in > disp02.pw.out
....
mpirun -np 4 pw.x < disp20.pw.in > disp20.pw.out

disp01.pw.out から disp20.pw.out までの20個の出力ファイルから、ALAMODE付属のツールによって必要な情報を抜き出します。

python3 /usr/share/alamode/tools/extract --QE si222.pw.in *.pw.out > DFSET_cubic

これにより、DFSET_cubicに必要な情報が出力されます。以上の計算はとても時間がかかるので、先を急ぎたい方はすでに計算済みのデータ(DFSET_cubic)がALAMODEのサンプルの中に含まれるので、コピーしてくることもできます。

cp /usr/share/alamode/example/Si/reference/DFSET_cubic .

最後にSiの原子間力定数を3次の非線形係数まで含めて計算します。まず、入力ファイルを準備します。

cp si222.cubic.in si222.cubic_opt.in

によって雛形を準備し、si222.cubic_opt.inを編集します。修正点は以下の通りです。

１．&generalフィールドでMODE=optimizeに変更

２．&optimizeフィールドを作成して、中に DFSET = DFSET_cubic と FC2XML = si222.xml と記述（si222.xmlは調和項の原子間力で得たファイル）

修正後のファイルは以下のようになります。

&general
  PREFIX = si222_cubic
  MODE = optimize
  NAT = 64; NKD = 1
  KD = Si
/
&interaction
  NORDER = 2  # 1: harmonic, 2: cubic, ..
/
&cell
  20.406 # factor in Bohr unit
  1.0 0.0 0.0 # a1
  0.0 1.0 0.0 # a2
  0.0 0.0 1.0 # a3
/
&cutoff 
  Si-Si None 7.3
/
&optimize
  DFSET = DFSET_cubic
  FC2XML = si222.xml
/
&position
  1 0.0000000000000000 0.0000000000000000 0.0000000000000000   
  1 0.0000000000000000 0.0000000000000000 0.5000000000000000
  (中略)
  1 0.8750000000000000 0.8750000000000000 0.1250000000000000
  1 0.8750000000000000 0.8750000000000000 0.6250000000000000
/

次にALMを実行します。

alm si222.cubic_opt.in > si222.cubic_opt.log

これにより、原子間力の情報が si222_cubic.fcs と si222_cubic.xml に出力されます。

７．熱伝導度の計算

Siの非線形フォノンの情報が得られたので、最後にこれを用いてSiの熱伝導度を計算してみましょう。まず入力ファイルを作ります。

cp si_phdos.in si_RTA.in

としたあと、si_RTA.inを編集します。修正点は以下の通りです。

１．&generalセクションでPREFIX, MODE, FCSXMLを以下のように変更

  PREFIX = si222_cubic 
  MODE = RTA
  FCSXML = si222_cubic.xml

２．&generalセクションで DETA_E = 1 を DT = 1.0に修正

３．&kpointセクションで40 40 40を10 10 10に修正(計算は2次の係数の計算に比べて重いので、最初は少ないk点数にしたほうがよい)

入力ファイルsi_RTA.inは以下のようになります。

&general
  PREFIX = si222_cubic
  MODE   = RTA
  FCSXML = si222_cubic.xml
  NKD = 1; KD = Si
  MASS = 28.0855
  DT = 1.0
/
&cell
  10.203
  0.0 0.5 0.5
  0.5 0.0 0.5
  0.5 0.5 0.0
/
&kpoint
  2
  10 10 10
/

&cell部分がプリミティブセルの指定になることに注意してください。ANPHONを実行します。

anphon si_RTA.in > si_RTA.out

データの解析には si222.result を使います。このファイルがある場合はリスタート計算になるので、k点を変えて再計算を行う場合は削除するかファイル名を別のものに変更してください。この結果だと絶対零度で熱伝導度が発散しますが、実際は試料の有限サイズ効果(界面散乱の効果)を取り込む必要があります。これは

python3 /usr/share/alamode/tools/analyze_phonons.py --calc kappa_boundary --size 1.0e+6 si222_cubic.result > si222_boundary_1mm.kl

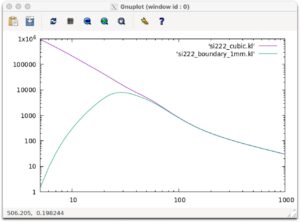
とすることで計算できます。これらの計算結果を出力してみましょう。

set log x
set log y
plot [5:1000] 'si222_cubic.kl' w l,'si222_boundary_1mm.kl' w l

以下のようなグラフがでれば成功です。縦軸はW/mKです。

TOP