HPhiを使った有限温度計算 その2(cTPQ)
Last Update:2023/05/11
はじめに
前回は、ミクロカノニカル分布に基づいた (micro-canonical Thermal Pure Quantum state, mTPQ)に基づいたKitaev模型の有限温度の計算を行いました。 HPhiでは、ミクロカノニカル分布だけではなく、カノニカル分布での有限温度の計算をすることができます。今回は、canonical Thermal Pure Quantum state (cTPQ)に基づいた1D Heisenberg模型の有限温度の計算を行います。mTPQと比較した時に、cTPQは低温領域の比熱を調べることは得意という特徴があります。
まずは、チュートリアルからサンプルファイルを用意します。
Git clone https://isspns-gitlab.issp.u-tokyo.ac.jp/hphi-dev/hphi-gallery.git
cd /hphi-gallery-main/data/tutorial/1_zero_temperature/1.6HPhi version 3.5.1では、cTPQはエキスパートモードでの計算になりますが、入力データを簡単に用意するファイルが用意されています。以下では、周期境界条件、L=12の場合のinput.txt, pair.txtの例を示します。
(input.txt) Ns 12 exct 2
(pair.txt) 0 1 x x 1 0 1 y y 1 0 1 z z 1 1 2 x x 1 1 2 y y 1 1 2 z z 1 ~~~~~~~~~~ 11 0 x x 1 11 0 y y 1 11 0 z z 1
入力ファイルが出来次第、以下のpythonファイルを実行します。
python MakeDef.py続いて、計算方法の指定をします。cTPQの場合、\(S_{z}\)を保存する必要があるため, CalcModel: Spin, CalcType: cTPQで指定します。
(calcmod_tpq.def), #CalcType = 0:Lanczos, 1:TPQCalc, 2:FullDiag, 3:CG, 4:Time-evolution #CalcModel = 0:Hubbard, 1:Spin, 2:Kondo, 3:HubbardGC, 4:SpinGC, 5:KondoGC #Restart = 0:None, 1:Save, 2:Restart&Save, 3:Restart #CalcSpec = 0:None, 1:Normal, 2:No H*Phi, 3:Save, 4:Restart, 5:Restart&Save CalcType 5 CalcModel 1 ReStart 0 CalcSpec 0 CalcEigenVec 0 InitialVecType 0 InputEigenVec 0 OutputEigenVec 0
計算で使用するパラメータを指定します。
(modpara.def) -------------------- Model_Parameters 0 -------------------- HPhi_Cal_Parameters -------------------- CDataFileHead zvo CParaFileHead zqp -------------------- Nsite 12 2Sz 0 Lanczos_max 2000 initial_iv -1 exct 8 LanczosEps 14 LanczosTarget 2 LargeValue 50 NumAve 10 ExpecInterval 20
全ての編集が終わったら、以下のコマンドで実行することでcTPQの計算ができます。大体、計算が終わるのは4~5分でしょうか。
[PathToHPhi] -e namelist_tpq.def続いて、後処理の平均を取るスクリプトは以下になります。
sh tutorial/2_finite_temperature/2.1/Aft_cTPQ.shこのスクリプトは平均値とエラーをブートストラップ法で推定することができます。比較のために、厳密対角化による1D Heisenberg模型の比熱も計算しておきます。
[PathToHPhi] -s tutorial/2_finite_temperature/2.1/stan1.in
python Finite.py例えば、Gnuplotを使うと
Gnuplot$se log x $se colors classic $se xlabel "T/J" $se ylabel "C" $plot "BS_MaxBS5.dat" u 1:4:5 w e lt 1 ps 1 pt 6 ,"FullDiag.dat" u 1:3 w l
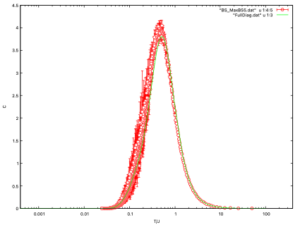
cTPQと厳密対角化の結果が大体一致していることが確認できました。また、NumAveを上げることでエラーバーを小さくできます。今回紹介した方法で有限温度のKitaev模型をcTPQで計算することができます。

