DSQSSで一次元ハイゼンベルク模型の帯磁率・動的感受率を計算してみる
Last Update:2021/12/09
はじめに
DSQSSは連続時間量子モンテカルロ法の計算ライブラリである。フラストレーションのない格子上でのスピン系が計算できる(ボゾン系の計算も可能で、その場合は任意の格子に対する計算が可能)。最近になりver. 2が公開され、ユーザインターフェースが大幅に改善された。類似の計算ライブラリとしては、ALPSがあるが、入力ファイルの作成に少し癖があり、動的相関関数の計算に対応していない。DSQSSは直感的な入力ファイル形式を利用しており、動的相関関数の計算にも対応している点が最大の特徴となる。ここでは一次元ハイゼンベルク模型の動的相関関数を計算してみよう。計算環境はMateriApps LIVE!を想定しているが、DSQSSは多くの計算環境でも同様にインストール可能であるので、ぜひ試していただきたい。
インストール方法
DSQSSはGitHubで公開されている。MateriApps LIVE!上でターミナルを開いて以下のコマンドを入力する。(以下、行頭の$ は端末のプロンプトを示している。)
$ git clone https://github.com/issp-center-dev/dsqss $ cd dsqss $ mkdir build $ cd build $ cmake -DCMAKE_INSTALL_PREFIX=../usr ../ $ make
テスト計算を実行するには下記のコマンドを入力する。
$ ctest
テストが無事通ったら、下記のコマンドで実行ファイルを-DCMAKE_INSTALL_PREFIXで指定されるディレクトリにコピーする。
$ make install
実行ファイルへのパスなどの設定を行うには、-DCMAKE_INSTALL_PREFIXで指定されるディレクトリの下のshareフォルダ内にあるdsqssvars-*.*.*.sh (*.*.*はバージョン名)を以下のように実行しておく。
$ source ../usr/share/dsqss/dsqssvars-*.*.*.sh
1次元ハイゼンベルク模型の帯磁率の計算
DSQSSに付属するサンプルファイルを利用して、1次元ハイゼンベルク模型(スピン1/2およびスピン1)の帯磁率の温度依存性を計算してみよう。ホームディレクトリにもどって、新しいディレクトリに移り、そこにサンプルプログラムをコピーする。
$ cd $ mkdir sus $ cd sus $ cp ../dsqss/sample/dla/02_spinchain/exec.py . $ python exec.py
この計算により、一次元ハイゼンベルグ模型(サイズ)帯磁率の温度依存性が2つのファイルxmzu_1.dat, xmzu_2.datに出力される(前者がスピン1/2, 後者がスピン1)。これをプロットするには、gnuplotを起動して以下のようにする。
$ gnuplot > plot "./xmzu_1.dat" u 1:2:3 w e,"./xmzu_2.dat" u 1:2:3 w e
これにより以下のようなグラフが得られる。
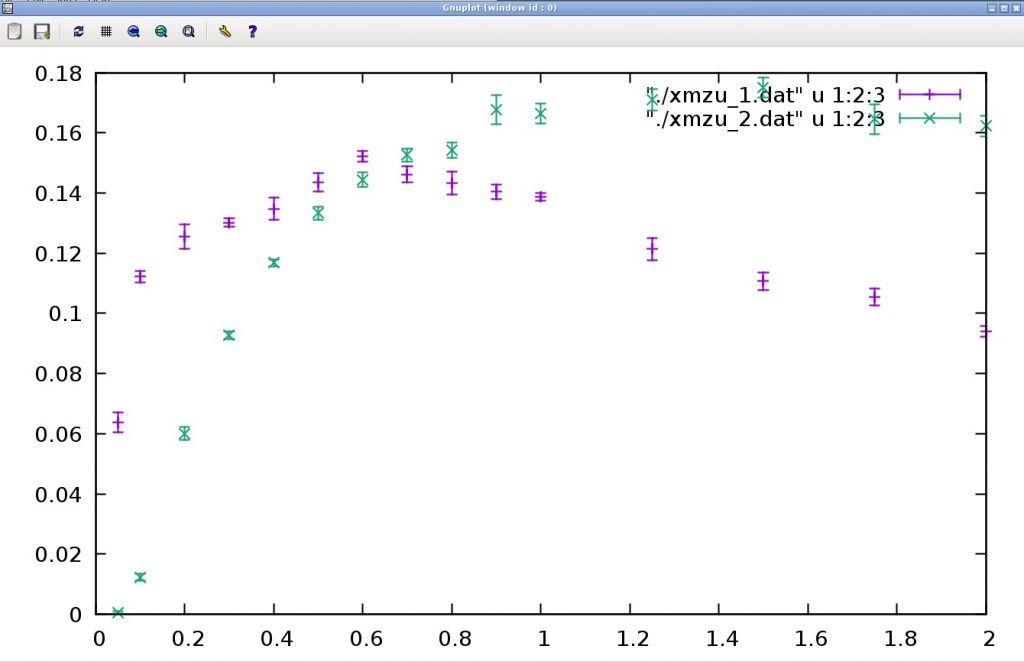
横軸が温度、縦軸が帯磁率である。スピン1/2のときに低温でほぼ一定の帯磁率となる(最低温で帯磁率が減少するのは有限サイズの効果である)。もとのターミナルにもどるには、
> exit
と打てば良い。
1次元ハイゼンベルク模型の動的感受率の計算
DSQSSの特徴である動的感受率の計算を行ってみよう。最も簡単な実行方法は「シンプルモード」を利用した計算方法である。このモードでは、.tomlファイルを作成するだけで、多くの模型の計算が可能である。まず、ホームディレクトリにもどって作業用ディレクトリを作り、そこに移動する。
$ cd $ mkdir sqw $ cd sqw
次に入力ファイル(ファイル名をstd.tomlとする)を作成する。具体的には、
$ emacs std.toml -nw
として、エディタを立ち上げて下記のファイルを打ち込む、もしくは、カットアンドペーストする。(保存するには、Ctrl-X Ctrl-S、エディタを終了するには、Ctrl-X Ctrl-Cを打つ。Ctrlはcontrolキーを押しながらの操作。)
[hamiltonian] model = "spin" M = 1 Jz = -1.0 Jxy = -1.0 h = 0.0 [lattice] lattice = "hypercubic" dim = 1 L = 32 bc = true [parameter] beta = 16.0 nset = 5 npre = 1000 ntherm = 1000 ndecor = 1000 nmcs = 10000 ntau = 256 seed = 31415 wvfile = "Sqtau.xml" [kpoints] ksteps = 1
ここでは32スピン系の逆温度β=16の計算を行っている(詳しいパラメータの情報はマニュアルを参照)。このファイルを保存後、同じディレクトリ内で以下のコマンドを実行する。
$ dla_pre std.toml
これを実行すると、DSQSSの計算に必要な入力ファイル(param.in, algorithm.xml, lattice.xml, Sqtau.xml)が生成される。量子モンテカルロの計算は下記のコマンドを実行する。(10分程度で終わるはずである。)
$ dla param.in
並列実行環境が整っている場合は、下記のコマンドにより並列計算が可能である。(乱数の種を変えてモンテカルロサンプルを増やす並列計算を自動で行い、エラーバーが小さくなる。コマンド名mpiexecは環境によって変わる可能性があるので注意。)
$ mpiexec -np 4 dla param.in
-npのあとの数字は並列数である。実行後、sample.logに基本的な物理情報が格納され、虚時間相関関数のファイルはck.datファイルに格納されている。これを適当な手法によって解析接続して、動的構造因子S(q,w)を計算する。ここではパデ近似による解析接続を行うpythonコードを用いよう。
このコードをブラウザからダウンロードして上記の計算の出力ファイルのあるディレクトリ(~/sqw)に保存する。その後、下記のように実行する。
$ python3 pade.py > chi.dat
これでchi.datに動的相関関数が出力される(各行には波数, 振動数, 動的相関の実部, 動的相関の虚部の順で数値が出力される)。これをgnuplotから描画するには以下のようにする。
$ gnuplot > set pm3d map > set palette rgbformulae 33,13,10 > splot [] [] [-1:3] 'chi.dat' u 1:2:4
計算が無事終わっていれば、下記のような図が表示されるはずである。横軸が波数(原点が1ずれていることに注意)、縦軸が振動数(エネルギー)であり、明るい場所が動的相関関数の虚部が大きい場所である。まだ計算精度は甘いが、一次元ハイゼンベルグ模型での基本的なモード分散(des Cloizeaux-Pearsonモード)が現れていることがわかる(並列度や乱数によって結果が少し変わる可能性があります)。
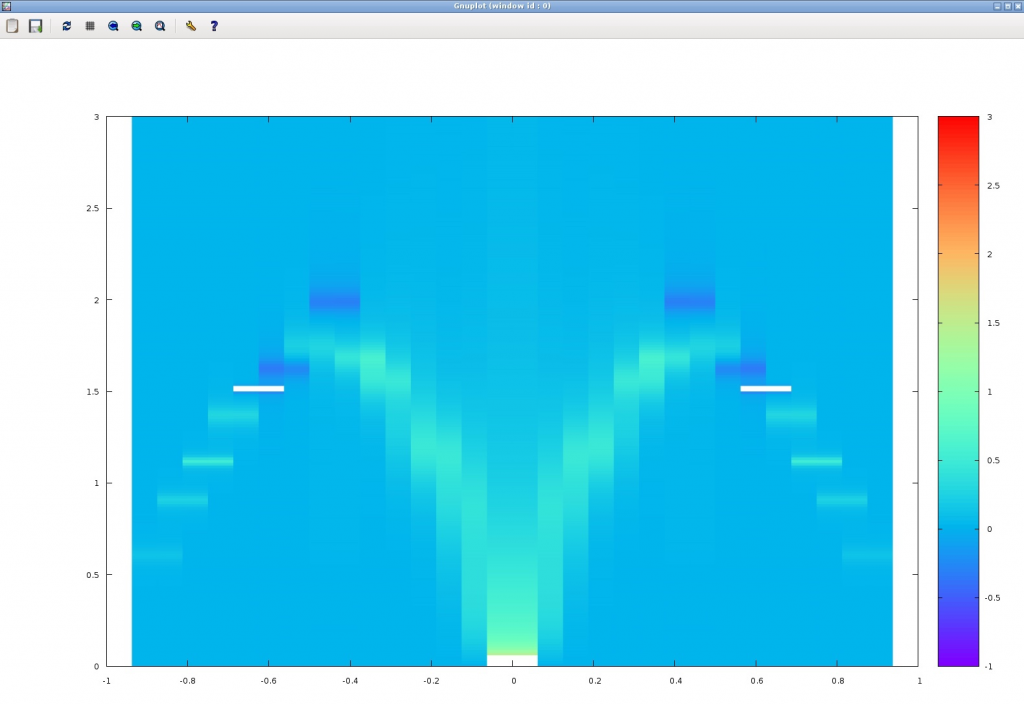
おわりに
解析接続によって動的相関関数を精度よく求めるのは一般に難しく、モンテカルロサンプルの数を十分大きくして精度のよいデータを用意する必要がある。一方、定性的な振る舞いだけであれば、比較的軽い計算だけで得られる。HPhiによる厳密対角化を用いた動的構造因子の計算(レビュー参照)と比較してみると興味深いであろう。

