ALPSを使ったQMC計算例
Last Update:2021/12/09
-
はじめに
ALPSは密度行列くりこみ群(DMRG)や厳密対角化(ED)、量子モンテカルロ(QMC)などの強相関系のための数値計算手法が実装されているライブラリ集です。チュートリアルが充実しているため、これらの手法に関わってこなかった方でも比較的簡単に実行できるようになっています。
ここではMateriApps LIVE! (MAL)を用いて、QMCのフラストレーションのある量子スピン系への適用を紹介します。MALとは様々な物性科学アプリがおさめられているLive Linux システムのことです。MALを使うことによってインストール作業を行わなくてもALPSを試してみることができます。詳細な使用法についてはMALのWikiが参考になります。使用したMALのバージョンはver. 2.0です。

フラストレーションのある量子スピン系として、今回は右図のような正方格子上のJ1-J2Heisenberg模型のシミュレーションを行って見ます。QMCは統計誤差の範囲内で厳密な手法ですが、フラストレーションがあると負符号というものが生じてモンテカルロ計算がうまくできないといった問題があります。解析例では、その符号がフラストレーションの強さによってどのように変化するのかを確認して見たいと思います。
-
実行方法
それでは、実際にALPSを動かしてみたいと思います。System toolsからLXTerminalを起動し、HOMEディレクトリ下にサンプルディレクトリをコピーし移動します。
mkdir alps_qmc cd alps_qmc
続いて、実行用のPythonスクリプトを用意します。wgetを使ってスクリプトfrustrated_qmc.pyをダウンロードして、テストディレクトリalps_qmcに持ってきてください。このスクリプトはチュートリアルサイトにあるtutorial8a.pyをもとに作っています。そのため、スクリプトの説明はチュートリアルサイトを参考にしてください。
wget https://ma.issp.u-tokyo.ac.jp/wp-content/uploads/sites/3/2018/12/frustrated_qmc.py
最後に下記のコマンドを打つと、先ほどダウンロードしたスクリプトを用いた計算が実行されます。
python frustrated_qmc.py
だいたい数分程度でプログラムが終了すると思います。
-
実行結果
スクリプトを実行するとした図のような結果が出力されます。これはモンテカルロで使う確率分布の符号の温度依存性です。凡例では“J1=***”となっていますが、ここでの“J1”は模型でいう“J2/J1”です。“J2/J1=1e-5”とありますが、これは“J2/J1 =0.0”とすると符号の期待値が出力されないためこのようにしています。なお、計算の出力自体は実行ディレクトリ直下にされます。温度”T”は最近接交換相互作用”J1”で規格化(T/J1)されています。
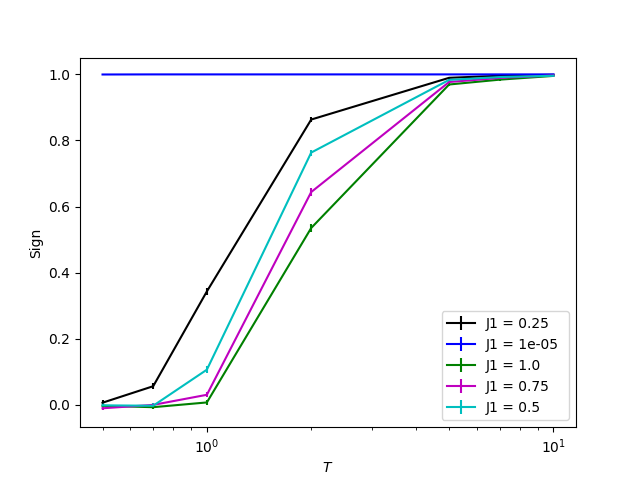
符号の温度依存性
上の図を見ると、フラストレーションが導入されると低温側で符号が0になってしまっています。これは確率の正負がどちらもほぼ等確率に出てきてしまって、モンテカルロ計算がうまく行えていないことを示しています。符号の図を閉じると、エネルギーの温度依存性も出力されますが、モンテカルロ法がうまくいっていないことががよくわかります。これがいわゆる負符号問題というものです。これを解決できれば、計算物理界隈でヒーローになれます。Let’s challenge!
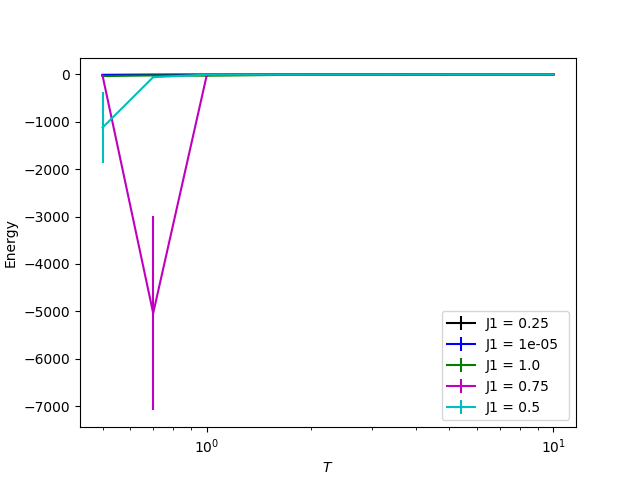
エネルギーの温度依存性
-
終わりに
ここではALPSを用いたQMC計算の例を紹介しました。DMRGやEDを用いた計算方法や他のQMCの計算例については、チュートリアルサイトを参考にしてください。

