AkaiKKRを用いた磁性半導体の磁性および自己組織化ナノ構造のシミュレーション
磁性半導体は磁性不純物(たとえばMn)をGaAsやInAsなどの半導体に高濃度に添加した物質で、強磁性を示しさらにその強磁性をキャリア濃度の変調により制御できることから半導体スピントロニクスの基礎材料として研究されています。不純物がランダムに結晶中に分布しているので、並進対称性を仮定する通常のバンド計算では扱いにくい系のひとつです。このような、不規則性を持つ系の計算によく用いられる方法としてコヒーレントポテンシャル近似(Coherent potential approximation; CPA)がありますが、グリーン関数を用いるバンド計算法、Korringa-Kohn-Rostoker(KKR)法と組み合わせて第一原理から不規則合金の電子状態計算が可能で(KKR-CPA法)、AkaiKKRコードとして公開されています。この方法の典型的な応用例として、磁性半導体の磁気的性質の予測が筆者のグループでおこなわれ、典型的な磁性半導体について精度の良いキュリー温度の計算が可能であることが示されました(図1)[1]。この計算では、GaAs中のMn間に働く有効交換相互作用を計算しモンテカルロ法でキュリー温度を見積もっています。KKR法は系のグリーン関数を計算する方法で、その特色は上記の様な不規則系や不純物および欠陥を含む系の計算、電子輸送現象の計算、オーダーN計算(遮蔽KKR法として知られています)などに活かされています。最近の磁性半導体に関する実験では、様々な磁性半導体中で磁性不純物が析出し、合成条件によりナノ構造を自己組織化することが知られていますが、そのような現実の材料でおこる複雑な現象についてもシミュレーションが可能となっており(図2)、実験研究の解釈や新しい機能をもつ材料の設計に応用されつつあります[2, 3]。ここで紹介した計算には、通常の汎用計算機クラスターが用いられています。
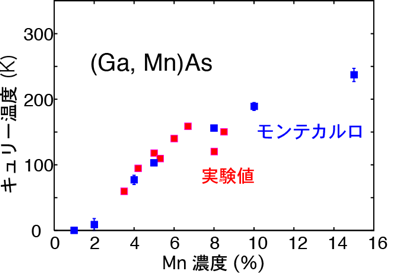
図1:KKR-CPA法で見積もった相互作用を用いたモンテカルロ計算によるMn添加GaAsのキュリー温度の計算値と実験値の比較(参考文献:[1])

図2:Cr添加ZnTeにおけるCrの自己組織化シミュレーション(参考文献[2])
参考文献:
[1] K. Sato, L. Bergqvist, J. Kudrnovský, P. H. Dederichs, O. Eriksson, I. Turek, B. Sanyal, G. Bouzerar, H. Katayama-Yoshida, V. A. Dinh, T. Fukushima, H. Kizaki, and R. Zeller, Rev. Mod. Phys. 82, 1633 (2010).
[2] T. Dietl, K. Sato, T. Fukushima, A. Bonanni, M. Jamet, A. Barski, S. Kuroda, M. Tanaka, Pham Nam Hai, and H. Katayama-Yoshida, Rev. Mod. Phys. 87, 1311 (2015).
[3] T. Fukushima, K. Sato, H. Katayama-Yoshida and P. H. Dederichs, Jpn. J. Appl. Phys. 45, L416 (2006)

