物質科学シミュレーションのポータルサイト

DSQSSはワーム更新法による量子モンテカルロ法です。フラストレーションのないスピン系やボゾン系に対応しており、特に、並列化可能なワーム更新量子モンテカルロ法によって、非常に大きいシステムサイズでのspin-1/2 XXZ模型やハードコアボゾン模型を計算することができます。ここでは、ハードコアボゾン模型の粒子数密度の化学ポテンシャル依存性を見ていきます。

まずは、サンプルファイルを用意します。

git clone https://github.com/issp-center-dev/dsqss
cd dsqss/sample/dla/03_bosesquare

二次元のハードコアボゾン模型
\[H = -t\sum_{\langle i,j \rangle}b_{i}^{\dagger}b_{j} +V\sum_{\langle i,j \rangle}n_{i}n_{j} +\mu\sum_{i}n_{i}\]
には、サンプルファイルが用意されています。

(exec.py)

V = 3
L = [8, 8]
beta = 10.0

lattice = {"lattice": "hypercubic", "dim": 2, "L": L}
hamiltonian = {"model": "boson", "t": 1, "V": V, "M": 1}

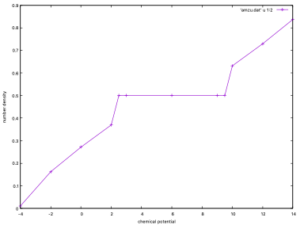
ここでは、パラメータ\(V/t=3, \beta =10\)を固定して,化学ポテンシャル\(\mu\)を\([-4\textrm{~}14]\)の区間で振っています。
以下で実行することができます。

python exec.py

計算後、amzu.datに密度の期待値と誤差が記録されているはずです。例えば、gnuplotを使うと,

gnuplot

$set xlabel "chemical potential"
$set ylabel "number density"
$plot 'amzu.dat' u 1:2 w lp

粒子数密度の化学ポテンシャル依存性を見ることができ、\(\mu = 3\textrm{~}9\)の区間にプラトーが出ることが確認できます。