HPhiでの実時間発展
Last Update:2023/05/11
1.はじめに
熱揺らぎによる相転移については確立した理論がありますが、実時間発展に伴う動的な相転移というのはあまり理解が進んでいません。例えば、量子系を実時間発展させると、あたかも熱平衡状態の臨界現象のような、クリティカルな時間で物理量に特異性を見ることができます。
ここでは、HΦ(HPhi)を使った一次元横磁場イジング鎖
\[ H(t)=\sum_{\langle i,j\rangle} S^{z}_{i} S^{z}_{j}+\sum_{i} \Gamma(t) S_{i}^{x} \]
の一例を紹介します。HΦ(HPhi) は、ハバード模型や量子スピン模型の厳密対角化ソルバーです。HPhi を用いることで、これらの基底状態や有限温度での計算もすることができますが、今回はクエンチダイナミクスでの磁化の特異性について確認していきます。
2.実行方法
まずは、基底状態を確認します。HOMEディレクトリ下に以下を作成します。
(stan1.sh)
model = "SpinGC"
method = "Time-Evolution"
lattice = "chain"
L = 12
Jz = -1.0
Gamma = 0.5
h = 1e-5
EigenvecIO = "in"
dt = 0.01
lanczos_max = 1000
SpinGCはグランドカノニカル集団でのハイゼンベルグ模型を示しています。今回の場合、イジング相互作用のみにしたいので縦磁場を\(h=1e-5\)としています。また、初期値の横磁場\(\Gamma_{t=0}\)は\(0.1\)に設定されており、 この場合\(\Gamma\)を\(0\rightarrow 0.6\)にクエンチしています。
次のコマンドを実行します。
HPhi -s stan1.in実行後、磁化の実時間発展はoutput/Flct.datに格納されます。動的相転移を見るには\(\Gamma\)をいくつか振る必要があります。以下では、パラメーター\(\Gamma= 0.2,0.5,0.6,1.2\)で振った後の結果をoutput/Flct_gamma=x.datと名前を変更してあげてから、プロットします。
コマンドライン上でgnuplotを起動させます。
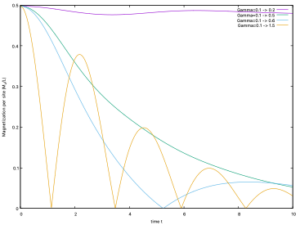
gnuplot$gnuplot> set xlabel "time t" $gnuplot> set ylabel "Magnetization per site |M_z/L|" gnuplot>p "output/Flct_gamma0.2.dat" u 1:(abs($6/12)) w l tit "Gamma=0.1 -> 0.2","output/Flct_gamma0.5.dat" u 1:(abs($6/12)) w l tit "Gamma=0.1 -> 0.5","output/Flct_gamma0.6.dat" u 1:(abs($6/12)) w l tit "Gamma=0.1 -> 0.6","output/Flct_gamma1.5.dat" u 1:(abs($6/12)) w l tit "Gamma=0.1 -> 1.5"
とすると、以下のように磁化の時間発展の図をプロットすることができます。図のように、\(\Gamma=0.6\)のあたりから一定の周期で特異点を持つ磁化を見ることができます。