mVMCを使った一次元近藤格子模型
Last Update:2023/05/11
一次元近藤格子模型は重い電子系の基礎的なモデルの一つであり、その基底状態にはリッチな相転移現象があることが知られています。
\[H = -t\sum_{\langle i,j \rangle,\alpha} c_{i,\alpha}^{\dagger} c_{j,\alpha} +J\sum_{j}S_{cj}\cdot S_{j}\]
今回はmVMCを使ってスピンと電荷の相関関数を計算することでその基底状態を調べます。mVMCは変分法に基づくモンテカルロ法であり、厳密対角化法では難しいシステムサイズに対しても高精度な計算をすることができます。
まず、Gitを使ってサンプルファイルを用意します。
git clone https://github.com/issp-center-dev/mVMC-tutorial.git
cd mVMC-tutorial/HandsOn/2022_1128/Samples/1D_Kondo今回はエキスパートモードでの計算になるのですが、MakeInput.pyとinput.tomlを使うことで簡単に設定することができます。
mVMC-tutorial/HandsOn/2022_1128/Samples/1D_Kondo/input.toml [lattice] Lx = 8 Ly = 1 Lz = 1 orb_num = 2 model_type = "Kondo" [mVMC] sub_x = 2 sub_y = 1 sub_z = 1 [mVMC_aft] modpara = "modpara.def" directory = "aft"
今回は、システムサイズL=8でHalf-Fillingの場合を調べるので、orb_num=2になっています。
編集が出来次第、以下の通りに実行します。
python MakeInput.py input.toml低密度領域や強結合領域を見る場合には、stan_opt.in& stan_aft.inの中の”J,Ncond”を変える必要があります。
(stan_opt.in) L = 8 Lsub = 2 lattice = "chain" model = "Kondo" t = 1.0 J = 4.0 ncond = 8 2Sz = 0 NVMCSample = 200 NSROptItrStep = 600 NMPTrans = 1 NSPStot = 0
入力ファイルから変分波動関数の最適化をします。
{PathTo/vmcdry.out} ./stan_opt.in
{ PathTo/vmc.out} namelist.def
cp ./output/zqp_opt.dat.
計算が終了するまでに、5〜6分程度かかるかと思います。また、必要な場合には、mpiexec -np ノード数 { PathTo/vmc.out} namelist.defで並列化をすることができます。
続いて、一体・二体グリーン関数の計算は以下で実行することができます。
{PathTo/vmcdry.out} } ./stan_aft.in
cp green1 greenone.def
cp green2 greentwo.def
{ PathTo/vmc.out} namelist.def ./zqp_opt.dat計算終了後、計算結果/outputを/aftに移動させます。
mv output aft最後に得られた物理量をサンプリングするには、以下で実行できます。
python VMClocal.py input.toml
python VMCcor.py input.tomlたとえば、Gnuplot を使うとプロットすると
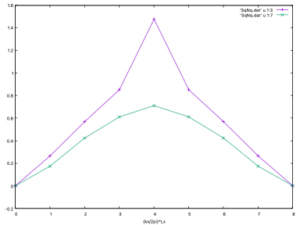
gnuplot$p 'SqNq.dat' u 1:3 w lp, 'SqNq.dat' u 1:7 w lp
これらはスピン・電荷構造因子に対応しています。 Half-Fillingの場合、スピン(紫)・電荷(緑)の両方で中央にピークが立ち、常磁性を確認することができます。