mVMCを使ったJ1-J2 Heisenbergモデルの計算
Last Update:2023/05/11
J1-J2 Heisenberg modelは最近接と次近接に相互作用を持つ量子スピン系です。
\[ J_{1}\sum_{\langle i,j\rangle}S_{i}S_{j} + J_{2}\sum_{\langle\langle i,j\rangle\rangle}S_{i}S_{j}\]
この模型はパラメーターJ2/J1 をうまく変えることで中間層に、長距離磁気秩序やダイマー秩序を持たない量子スピン液体状態が実現すると予想されています。特に、\(0.4 <J2/J1 < 0.6\) の区間で、熱力学極限(\(L\rightarrow \infty\))でスピン液体が実現するのかは今の所分かっておらず、現在でも多くの研究がなされている模型です。
今回はmVMCを使った低エネルギー領域での比較的に大きいシステムサイズで計算を行います。同様の計算をHPhiですることができますが, 変分法に基づくモンテカルロ法mVMCを使うことで、厳密対角化法では難しいシステムサイズに対しても高精度な計算をすることができます。 ここではHPhiと計算結果を確認しながら、J1-J2 Heisenberg modelのスピン構造因子を計算していきます。
まず、Gitを使ってサンプルファイルを用意します。
git clone https://github.com/issp-center-dev/mVMC-tutorial.git
cd mVMC-tutorial/HandsOn/2022_1128/Samples/2D_J1J2Heisenberg変分波動関数の最適化
まずは、小さいシステムサイズ L = 4の入力ファイルを用意します
(Samples/2D_J1J2Heisenberg/stan_opt.in) W = 4 Wsub = 2 L = 4 Lsub = 2 lattice = "square" model = "Spin" J = 1.0 J' = 1.0 2Sz = 0 NVMCSample = 200 NSROptItrStep = 600 NMPTrans = 1 NSPStot = 0
vmcdry.outで必要な入力ファイルを作成し、vmc.outで最適化を行うことができます。
Path to /vmcdry.out stan_opt.in
Path to /vmc.out namelist.def最適化自体は3-4分で終わるはずです。mVMCは厳密なアルゴリズムではないので、エネルギーの収束を確認します。
gnuplot$ plot “./output/zvo_out_001.dat” u 1

縦軸がエネルギー、横軸が最適化の反復回数です。収束が悪い場合には適宜NVMCSampleや NSROptItrStepを変更してください。
一体・二体グリーン関数の計算
スピン構造因子に必要な一体・二体グリーン関数の計算を先ほど得られた波動関数から計算します。
Path to /vmcdry.out stan_aft.in
cp green1 greenone.def
cp green2 greentwo.def
Path to /vmc.out namelist.def ./zqp_opt.dat./outputにはzvo_out_xxx.dat (エネルギー、そのvariance), zvo_cisajs_xxx.dat (一体グリーン関数), zvo_cisajscktalt_xxx.dat(二体グリーン関数)が生成されるはずです。物理量の統計的な後処理は
mv output aft
python VMClocal.py input.toml
python VMCcor.py input.tomlで計算することができます。
実行結果
Gnuplotを起動させ、以下のコマンドでスピン構造因子をプロットすることができます。
gnuplot> set xlabel "q_{x}/pi"
gnuplot> set ylabel " q_{y}/pi "
gnuplot> set zlabel " S(q) "
$splot “SqNq.dat” u 1:2:3 w lp

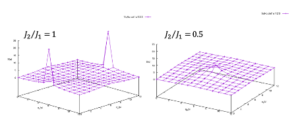
今回の場合はJ2/J1 = 1なので 実空間の端にピークがたち、反強磁性ストライプ型の磁気秩序を示しており、同様の計算をstan_opt.inのJ’=0.5 にすると中心になだらなピークがたちます。 HPhiの結果(https://issp-center-dev.github.io/HPhi/manual/develop/tutorial/en/html/zero_temperature/J1J2.html)を見ると、概形が一致していることが確認できます。また、L=12までシステムサイズを上げるとピークの違いがはっきりします。