DC を用いた、MP2法(電子相関を含む波動関数理論)に基づく大規模分子の構造計算
分子や固体の電子状態計算で、現在広く普及している計算法は、密度汎関数理論(DFT)です。DFTは実効的な計算コストと精度のバランスが良く、大変優れた方法ではありますが、計算に用いる「汎関数」の種類によって結果が変わる上、絶対的に優れた汎関数というものは存在しません。量子化学の世界では、波動関数理論という伝統的で系統的な体系があり、こちらの理論では精度を高めるための明確な指針が決まっています。しかし、最低限の精度に必要な電子相関を含むMP2法であっても、特に大きな分子の計算にはDFTに比べると膨大な時間が必要になります。さらに、分子構造を決定するためのエネルギー勾配計算に追加で必要となるコストも、DFTに比べて非常に大きく、大きな系でこれを実現するのは困難でした。
私たちは、波動関数理論に基づく大規模分子の電子状態計算を実現するため、計算時間を劇的に減らす分割統治(divide-and-conquer: DC)計算理論と、その計算プログラム「DC」の開発、適用を行っています。理論の概要については、こちらのページを参照して下さい。
図はモデル分子であるポリエン(CnHn+2)のDC-MP2エネルギー勾配計算を実行したときの計算時間(上)と要求されるメモリ容量(下)を示しています[1]。通常の方法では分子の大きさ(横軸)が大きくなると、計算時間、メモリ容量ともに急激に増加しますが、DCを用いた場合には計算時間は線形に、またメモリ容量は一定に抑えることができます。この計算は、PC 1ノードを使った結果ですが、DC-MP2計算は効率的な2段階の階層的並列計算法の開発[2]もされており、京での稼働実績もあります。MP2法をはじめとする波動関数理論は、生体分子などで極めて重要でありながら、DFTでは経験的にしか取り扱うことができない分散力を非経験的に取り込むことができるため、タンパク質の計算などにも応用されています[3-5]。
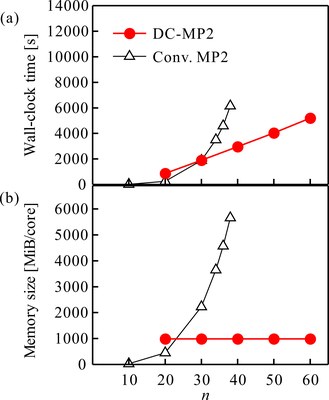
図:ポリエンCnHn+2のDC-MP2エネルギー勾配計算に要した(a)計算時間と(b)メモリ容量。
[1] M. Kobayashi and H. Nakai, J. Chem. Phys. 138, 044102 (2013).
[2] M. Katouda, M. Kobayashi, H. Nakai, and S. Nagase, J. Comput. Chem. 32, 2756 (2011).
[3] P. Saparpakorn, M. Kobayashi, S. Hannongbua, and H. Nakai, Int. J. Quantum Chem. 113, 510 (2013).
[4] P. Saparpakorn, M. Kobayashi, and H. Nakai, Bull. Chem. Soc. Jpn. 86, 67 (2013).
[5] T. Yoshikawa, M. Kobayashi, A. Fujii, and H. Nakai, J. Phys. Chem. B 117, 5565 (2013).
