MateriApps
物質科学シミュレーションのポータルサイト

現在アプリ掲載数323件

お問合せ / アプリ掲載依頼
もっと詳しく探す

COMmon Bayesian Optimization Library (COMBO)

  • 公開度：3 ★★★
  • ドキュメント充実度：1 ★☆☆

機械学習で使われるベイズ最適化のPythonライブラリ。データ数に対して線形に計算コストが増大するので、大きな特徴空間でベイズ最適化を行うことが可能。ハイパーパラメータは第二種最尤推定に基づいてデータから自動的に学習される。

量子格子模型ソルバーHΦとベイズ最適化ライブラリCOMBOを組み合わせたモデル推定事例の紹介
Last Update:2021/12/09
あなたはすでに投票済みです！

執筆：吉見一慶 (2019/10/12)

(東京大学物性研究所)

  1. はじめに

2019/10/8-10に行った計算物質科学イノベーションキャンプで、ベイズ最適化ライブラリCOMBOと量子格子模型ソルバーHΦを利用し、1次元Heisenberg模型の模型推定を行う事例が紹介されました。ここでは、Macbook(Retina, 12-inch, 2017, 1.4 GHz Intel Core i7, 16 GB 1867 MHz LPDDR3)を用いて、その例について紹介します。なお、サンプルプログラムはHPhi-Garallyにアップロードしてありますので、興味のある方はぜひご覧ください。

 

  1. インストール・コンパイル方法(推奨)

まず、最初にHΦをこのページにしたがってダウンロード・インストールします。以下、HΦはPath_to_HPhiにダウンロードされたものとします。次にCOMBOをインストールします。HPhi-Garallyには、COMBOのインストールスクリプトがあるので、ここではそれを利用します。なお、COMBOのインストールはpython2環境である必要があるので注意してください。

$ git clone https://github.com/issp-center-dev/HPhi-gallery.git
$ cd ./HPhi-gallery/ModelEstimation/
$ sh ./install_combo.sh

これによりCOMBOがカレントディレクトリにインストールされます。また、HΦをカレントディレクトリにコピーしておきます。

$ cp Path_to_HPhi/HPhi .

これで準備は完了です。

 

  1. 実行方法

モデル推定の実行は非常に簡単で、

$python ./model_estimation.py

を実行するだけです。8分半程度でプログラムが終了すると思います。

 

以下、簡単にこのプログラムの内容について説明します。このプログラムでは、12サイト１次元Heisenberg鎖

$$H = \sum_{i=1}^{12} J_1 S_{i} \cdot S_{i+1} + J_2 S_{i} \cdot S_{i+2} + J_3 S_{i} \cdot S_{i+3}$$

のパラメータ推定をしています(ただし、\(S_i=S_{i+12}\))。プログラムの流れですが、最初にHΦを用いて(\(J_1, J_2, J_3\)) = (1.0, 0.5, 0.3)の磁化曲線をあらかじめ計算します。その後、各\(J\)に対して0から2までの間を0.1毎に刻んだ空間(\(21^3\))に対して、COMBOを用いてベイズ最適化を行い、最適解を探し出します。

 

次にmodel_estimation.pyの中身について簡単に説明します。

3.1 探索空間の定義(l.37-l.61)
#In
#Create candidate
window_num=20

J1_lower=0.0
J1_upper=2.0

J2_lower=0.0
J2_upper=2.0

J3_lower=0.0
J3_upper=2.0

X=[]

for i in range(window_num+1):
  for j in range(window_num+1):
    for k in range(window_num+1):

      X.append([round(J1_lower+(J1_upper-J1_lower)/window_num*i,3),
      round(J2_lower+(J2_upper-J2_lower)/window_num*j,3),
      round(J3_lower+(J3_upper-J3_lower)/window_num*k,3)])
3.2 ターゲットとする磁化曲線の取得
#target magnetization
input_dict = {}
input_dict["J0"] = 1.0
input_dict["J0'"] = 0.5
input_dict["J0''"] = 0.3
energy_list = HPhi_calc.get_energy_by_hphi(input_dict)

magnetic_field=[0.01*num for num in range(300)]

target=[]

for H in magnetic_field:
  target.append(HPhi_calc.get_mag(energy_list, H))

input_dictのキーワードでは、\(J0=J_1, J0’=J_2, J0’’=J_3\)に対応しています。input_dictの詳細はHPhi-Garallyにあるhphi_io.pyをご覧ください。基本的にはHΦのスタンダードモードの入力ファイルで使用しているパラメータを指定できます。これを用いることで、格子やモデルパラメータを簡単に変更できます。

3.3 パラメータ空間の正規化(l. 99-101)
# Normalize the mean and standard deviation along the each column of X to 0 and 1, respectively
X_normalized = combo.misc.centering( X )
3.4 シミュレータクラスの定義(l.108-144)

(\(J_1, J_2, J_3\))を与えた場合の正しい磁化曲線からのずれの2乗に-1を乗じたものを返すための関数__call__を定義しています。この関数がCOMBO内部で読み込まれ、スコアとして返されます。なお、COMBOではスコアが大きなものが最適解として選ばれるので、今の場合はずれが0となる相互作用の際に最高スコアとなるように、-1をかけています。

3.5 COMBOの実行

(1) l. 156

policy = combo.search.discrete.policy(test_X=X_normalized)

で、探索空間をCOMBOに渡します。

(2) l. 162

policy.set_seed( 111 )

乱数の種を設定します。

(3) l. 170

res = policy.random_search(max_num_probes=10, simulator=simulator())

ベイズ最適化を行うための前処理として初期パラメータ群をゲットするため、ランダムサーチをmax_num_probes回行います(今の場合は10回)。

(4) l.180-181

res = policy.bayes_search(max_num_probes=80, simulator=simulator(), score='TS',
interval=20,num_rand_basis=5000)

ベイズ最適化を行います。max_num_probes回パラメータ探索を行います。パラメータの学習はinterval回毎に行われます。num_rand_basisは基底関数の数を表します。

(5) l.198

best_fx, best_action = res.export_all_sequence_best_fx()

探索された最適解とその時のアクション（探索空間におけるパラメータ番号）を取得します。

(6) l. 200- (コードは省略)

最適なパラメータ、各ステップで選んだパラメータに対するスコアf(x)、アクション(パラメータ番号)、各ステップのベストスコアとそのアクションを出力するようにしています。

 

  1. 実行結果

計算の結果は標準出力に順次出されます。

4.1 各ステップでの状況
*********************
Present optimum interactions
J1= 0.4
J2= 0.3
J3= 1.0

0014-th step: f(x) = -352.000000 (action=3705)
current best f(x) = -106.000000 (best action=1837)
*********************

最初にその時のベストスコアである(\(J_1, J_2, J_3\))が表示されます。また、その下に選択されたスコアとアクション、またその時点でのベストスコアとアクションが記載されます。

 

4.2 ハイパーパラメータの学習

interval回毎にハイパーパラメータが学習され、以下のような情報が出力されます。

Start the initial hyper parameter searching ...
Done

Start the hyper parameter learning ...
0 -th epoch marginal likelihood 136.2168409123567
50 -th epoch marginal likelihood 135.94182130567467
100 -th epoch marginal likelihood 135.69734307091377
150 -th epoch marginal likelihood 135.49409229773718
200 -th epoch marginal likelihood 135.3394449330423
250 -th epoch marginal likelihood 135.23010176783998
300 -th epoch marginal likelihood 135.15595117152745
350 -th epoch marginal likelihood 135.1061048945242
400 -th epoch marginal likelihood 135.07201316618244
450 -th epoch marginal likelihood 135.04800861234918
500 -th epoch marginal likelihood 135.0306626271009
Done
4.3 計算結果の出力

計算が終了すると最適なパラメータが出力されます。今回の例では、無事に正しい解が推定されていることがわかります。

Estimated model parameter
J1= 1.0
J2= 0.5
J3= 0.3

また、ここでは省略しますが、続けて各ステップで選んだパラメータに対するスコアf(x)とアクション(パラメータ番号)、各ステップのベストスコアとそのアクションが出力されます。これらはcombo_res.datにも、上の順番で出力されます。下の図では、縦軸をcurrent best action、横軸をステップ数として表示しています。図の途中(64回目)から正しい解が得られていることがわかります。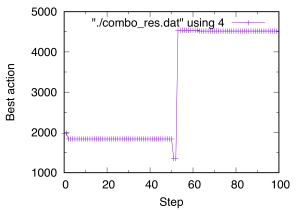

  1. 終わりに

ここではHΦとCOMBOを用いた簡単な計算例を紹介しました。デモンストレーションのため、小さい系での解析を行いましたが、東京大学物性研究所スーパーコンピュータシステムB sekireiを用いたより実践的な計算も可能なように、HPhi-GarallyのModelEstimation/sekirei下にCOMBOのインストールスクリプトとジョブ投入スクリプトのサンプルが置いてあります。興味をお持ちの方はぜひご利用ください。また、本サンプルについて質問がある方は、k-yoshimi_at_issp.u-tokyo.ac.jp(_at_を@に変更)までご連絡ください。

 

 

TOP