物質科学シミュレーションのポータルサイト

TeNeS [1] は２次元格子状で定義された量子系の基底状態を計算するために開発されました．TeNeS で採用している計算手法は波動関数に虚数時間発展演算子を作用させることで徐々に基底状態に近づけていくというもので，一般に Time-Evolving Block Decimation（TEBD）と呼ばれる手法です．波動関数はテンソルネットワークで表現されていて，計算量を発散させないために，有限のボンド次元の範囲内にとどめる近似を行います．このボンド次元が近似の精度を決めるパラメータになっています．熱力学極限の物理量を評価するための手法としては，他の多くの手法において計算する格子サイズが近似精度を決める一つのパラメータになっていますが，TeNeSでは格子サイズは無限大です．ただし，より高精度の計算をする場合には，ボンド次元が有限であることからくる誤差に関して外挿が必要です．この他の特徴としては，量子モンテカルロ法と比較すると，負符号問題がないこと，厳密対角化の計算量やメモリ必要量がサイズの指数関数で増えるのにたいして，TeNeS ではボンド次元の冪で押さえられることなどがあります．

2023年にリリースされた ver.2.0.0 では，実時間発展や有限温度計算もサポートされるようになっていますが，ここでは，このパッケージを使って，まず基本となる基底状態計算の事例を紹介します．例として，２＋１次元横磁場イジングモデルについて，横磁場の関数として，転移点で自発磁化が急激にゼロになる様子を計算してみることにします．

まず，インストール後に，

$ source <TENES_ROOT>/tenesvars-2.0.0-0.sh

などで，環境変数を整えたあと，

$ cp -rf $TENES_ROOT/sample/* .

For the 2+1 dimensional transverse field Ising model,として，手元にサンプルスクリプトを含んだフォルダをコピーします．そのあと，たとえば，２＋１次元横磁場イジングモデルの場合には，

$ cd 01_transverse_field_ising 
$ tenes_simple simple.toml 
$ tenes_std std.toml 
$ tenes input.toml

で実行されます．（物性研のプリインストール環境では，最後の３行に替えて，あらかじめ sample_jobscripts/tenes.sh などの名前で用意されている実行スクリプトを手元にコピーして，それをバッチジョブとしてサブミットするのが簡単です．）ここで，使用した最初の入力ファイル simple.toml は何も手を入れていない状態では，

hx = 0.0   # hx Sx

この実行によって，output というフォルダが新たに作られ，その中に計算結果が格納されています．今回のテスト計算に必要なスピンの z 方向成分の期待値が記録されているのは，output/onesite_obs.dat というファイルで，このなかの，

0 0 5.00000000000000000e-01 0.00000000000000000e+00

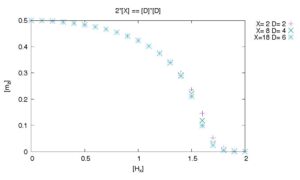
この図では，ボンド次元も (X,D)=(2,2), (8,4), (18,6) の３通りに変化させて計算しています．（X は角テンソルのボンド次元，D はバルクテンソルのボンド次元で，ともに近似精度をコントロールしています．一般には X を D の２乗に比例させることが自然なチョイスです．）これらのボンド次元も simple.toml のなかで定義されています．具体的には以下の行で定義されているので，ここを変えて計算を行うことで，上記のようなプロットに必要な計算結果が得られます．（このレビューでは使いませんでしたが，ver.2.0.0 の sample/01_transverse_field_ising フォルダの中には，上記のようなプロットを得るためのツール tutorial_example.py , tutorial_read.py も含まれています．）

dimension = 2  #  Bond dimension of corner transfer matrix

virtual_dim = 2 #   Bond dimension of bulk tensors