mptensor (v0.2) on sekirei (ISSP System B) (2020.02.01)
Last Update:2024/10/10
Introduction
Computation with tensor representation is the current fashion, with Google’s TensorFlow as a well-known example. Though with a much smaller market, computation in the tensor representation, known as the tensor network method, is a recent focus of attention in computational condensed matter physics, not only for its computational efficiency but also as a language for understanding topological phenomena in quantum many-body problems. Also in the field of the data science, usage of the tensor representation for data compression and feature extraction is being explored. While functions such as tensordot and linalg.svd in numpy are quite handy for small-scale computation, one may need something that may be equally handy but supports mpi parallelization. To meet such needs, Satoshi Morita at ISSP is developing mptensor. The latest version is v0.2 and only very limited documents come with the source codes. However, it is not so hard to find out the basic usage of the library by looking into the source codes of small example programs. The following is a report on our trial of mptensor on sekirei, ISSP’s main supercomputer.
Install
To begin with, we install mptensor(v0.2) on sekirei. To obtain the source codes, we do
$ git clone https://github.com/smorita/mptensor.git
Then, the source codes are stored locally. Now, let us go into the working directory by
$ mptensor> cd mptensor
and prepare for compilation by editing Makefile.option.
$ mptensor> emacs Makefile.option
Options for sekirei are already written (but commented-out) in Makefile.option. We just reactivate the following 4 lines (including the first one that is truly a comment).
##### ISSP System B (sekirei) ##### CXX = mpicxx CXXFLAGS = -O3 -xCORE-AVX2 -qopenmp -parallel LDFLAGS = -lmkl_scalapack_lp64 -lmkl_blacs_sgimpt_lp64 -mkl=parallel -lmpi
Now, we are ready to generate src/libmptensor.a.
$ mptensor> make
make -C src make[1]: Entering directory '/home/k0148/k014800/test_mptensor/mptensor/src' ar: creating libmptensor.a a - mptensor/tensor.o a - mptensor/index.o a - mptensor/scalapack/matrix_scalapack.o a - mptensor/scalapack/blacsgrid.o a - mptensor/rsvd.o a - mptensor/lapack/matrix_lapack.o a - mptensor/mpi_wrapper.o make[1]: Leaving directory '/home/kxxxx/kxxxxxx/mptensor/src'
Thus, we have successfully generated src/libmptensor.a.
Compiling the executable for testing the installation
Next, we generate the executable tensor_test.out for testing the installed library.
$ mptensor> cd tests
By editing Makefile in this directory, we specify the location of libraries related to blas.
$ mptensor/tests> emacs Makefile
Specifically, we insert the following line in the first part of Makefile.
LDFLAGS = -lmkl_scalapack_lp64 -lmkl_blacs_sgimpt_lp64 -mkl=parallel -lmpi
Then we make.
$ mptensor/tests> make
Now, the testing program tensor_test.out has been generated.
Editing the batch script file for executing the testing program
We then create a shelscript run.sh that is supposed to mpi execute tensor_test.out on sekirei. The script run.sh should contain the following.
#!/bin/bash #QSUB -queue i18cpu #QSUB -node 1 #QSUB -omp 1 #QSUB -place pack #QSUB -over false #PBS -l walltime=00:10:00 #PBS -N mptensor HDIR=/home/kxxxx/kxxxxxx/test_mptensor/mptensor export HDIR PATH=$HDIR/src:$PATH PATH=$HDIR/tests:$PATH export PATH mpijob tensor_test.out
Executing tensor_test.out
We throw the script run.sh into the job queue by
$ mptensor> qsub run.sh $ mptensor> qstat -u kxxxxx
We wait for the job to terminate, checking the job status from time to time by qstat command. (Since we are using the interactive queue, it must finish in a relatively short time.) In the end, the job finishes dumping the result into a file like mptensor.oxxxxxxx (with xxxxxxx being the job ID), which should contain something like
$ mptensor> cat mptensor.oxxxxxxx ======================================== Contract <complex> ( A[N0, N1, N0, N2], Axes(0), Axes(2) ) [N0, N1, N0, N2] = [10, 11, 10, 12] Error= 1.77636e-15 Time= 0.000138 [sec] Time(check)= 0.000156 [sec] ---------------------------------------- A: Tensor: shape= [10, 11, 10, 12] upper_rank= 2 axes_map= [0, 1, 2, 3] Matrix: prow= 0 pcol= 0 local_size= 960 lld(locr)= 30 locc= 32 ========================================
It seems the job was successful. Correct installation has been confirmed.
Computation of 2D Ising model by Tensor Renormalization Group (TRG) method
We can further try the mptensor library for a real physics problem. In the examples directory we can find some application programs including the TRG calculation of the free energy of the 2D Ising model. The TRG is the simplest renormalization group transformation with the tensor network representation. It was originally proposed by Levin and Nave (“Tensor Renormalization Group Approach to Two-Dimensional Classical Lattice Models”, PRL 99, 120601 (2007)).
Generating the executable file trg.out
Similarly to tests, we move to the working directory and edit Makefile to specify the location of the blas-related libraries.
$ mptensor> cd examples/Ising_2D> $ mptensor/examples/Ising_2D> emacs Makefile
We insert the following line.
LDFLAGS = -lmkl_scalapack_lp64 -lmkl_blacs_sgimpt_lp64 -mkl=parallel -lmpi
Then, we just make.
$ mptensor/examples/Ising_2D > make
We can confirm the two executable files.
$ mptensor/examples/Ising_2D > ls *.out hotrg.out trg.out
Both trg.out and hotrg.out are numerical RG transformations, though the ways the transformation is done are rather different. Since mptensor is for the basic tensor operations, such as the partial contraction and the tensor decomposition by the singular value decomposition (SVD), it can be used in a wide variety of applications. In the following, we focus on trg.out.
Executing trg.out
We do almost the same as tests. We first create the batch script file which is almost identical to the one we created for tests.
$ mptensor> emacs run.sh
We just copy “run.sh”, which we created for tests, as “run_trg.sh”, and add the following line in the path section.
PATH=$HDIR/examples:$PATH
Also, we change the last line into the following.
mpijob trg.out
When run_trg.sh is ready, we throw it to the batch queue.
$ mptensor> qsub run_trg.sh
After completion, we check the output.
$ mptensor> cat mptensor.oxxxxxxx # confirmation of the result ##### parameters ##### # T= 2.269185314 <-- the temperature is set to be the critical one # chi= 8 <-- the bond dimension # f_exact= -2.109651145 <-- the exact value of the free energy ##### keys ##### <-- the meaning of each column in the output section that follows # 1: step <-- the number of the RG transformations # 2: N_spin <-- the number of spins corresponding to the one renormalized site # 3: free energy (f) <-- the free-energy of the renormalized one-site system # 4: relative error ((f-f_exact)/|f_exact|) <-- the relative error ##### output ##### 0 1.000000e+00 -3.5728794027e+00 -6.9358778196e-01 1 2.000000e+00 -2.8193568384e+00 -3.3640902936e-01 2 4.000000e+00 -2.4859076215e+00 -1.7835009254e-01 3 8.000000e+00 -2.2892976961e+00 -8.5154624728e-02 4 1.600000e+01 -2.2011430750e+00 -4.3368274725e-02 5 3.200000e+01 -2.1548523417e+00 -2.1425910748e-02 6 6.400000e+01 -2.1323109230e+00 -1.0741007337e-02 7 1.280000e+02 -2.1209406219e+00 -5.3513479261e-03 8 2.560000e+02 -2.1152643697e+00 -2.6607361809e-03 9 5.120000e+02 -2.1124118689e+00 -1.3086164761e-03 10 1.024000e+03 -2.1109761387e+00 -6.2806310704e-04 11 2.048000e+03 -2.1102506060e+00 -2.8415188545e-04 12 4.096000e+03 -2.1098827582e+00 -1.0978760762e-04 13 8.192000e+03 -2.1096958939e+00 -2.1211683550e-05 14 1.638400e+04 -2.1096011032e+00 2.3720238913e-05 15 3.276800e+04 -2.1095532720e+00 4.6392793419e-05 16 6.553600e+04 -2.1095292808e+00 5.7764933470e-05
The free energy has been computed with the more than 4 digit precision!
How far can we go?
The most crucial parameter that determines the size and the precision of the calculation is the dimension of each index of the tensor, i.e., the bond dimension. By changing this parameter, we try to find out how large computation we can do. By looking into the source code of trg.cc, we find that trg.out takes three parameters, the bond dimension (chi), the number of renormalization group transformations (nstep), and the temperature (T) as command-line parameters. With this knowledge, we modify the shellscript we have used above and get something like the following.
#!/bin/bash
#QSUB -queue i18cpu
#QSUB -node 16
#QSUB -omp 1
#QSUB -place pack
#QSUB -over false
#PBS -l walltime=00:10:00
#PBS -N mptensor
#PBS -o mptensor.o.16node
#PBS -e mptensor.e.16node
HDIR=/home/kxxxx/kxxxxxx/test_mptensor/mptensor
PATH=$HDIR/examples/Ising_2D:$HDIR/tests:$HDIR/src:$PATH
export PATH
nstep=16
chilist=( "6" "12" "24" "48" "96" )
for chi in "${chilist[@]}"; do
echo >&2
command="time mpijob -np 384 trg.out ${chi} ${nstep}"
echo $command >&2
$command
done
By executing this script, we should obtain the elapsed times for 16 node (394 process) mpi-parallel calculations with the bond dimensions, 6, 12, 24, 48 and 96. The following is the output.
$ mptensor> more mptensor.e.16node time mpijob -np 384 trg.out 96 16 Usage: trg.out chi step T Warning: Assuming T = T_c 0.04user 0.02system 3:27.84elapsed 0%CPU (0avgtext+0avgdata 2100maxresident)k 0inputs+0outputs (0major+13450minor)pagefaults 0swaps
Now, we see that the largest calculation (chi=96) is finished in 3 minutes and a half. If I remember correctly, chi=20 was more or less the upper limit of the calculation on my PC with my own (totally unoptimized) code. Comparing to that, the result shows the power of the well optimized code and the high-performance hardware.
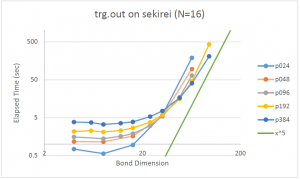
Finally, we show a figure plotting the computational (elapsed) time for various combinations of the number of processes and the bond dimensions. In the legend, “p024” means that 24 processors were used. We see that, for the small calculation, parallelization is not helpful; the computational time even increases as the number of processors increases. For larger calculations, however, the power of many processors are efficiently used in reducing the computational time. The green straight line in the figure is the ideal theoretical curve for the algorithm. It seems the measured CPU time approaches the slope of this line asymptotically, indicating that there is no essential redundancy in mptensor.
Summary
While the trg and the hotrg included in the package are for 2D Ising model, they can be used for any statistical mechanical model defined on square lattice with minor modifications. The mptensor library is for the partial contraction and the SVD decomposition of tensors, it can be used for wide variety of applications. For example, it can be used for quantum ground state calculation by the imaginary-time evolution method or the variational method, which is made public as another program package TeNeS.
#Revision History
– 2024/10/10 modify a hyperlink
