1. Introduction

Here I introduce how to use HPhi on MateriApps LIVE!. “MaterialApps LIVE!” is a Live Linux system with a variety of  apps for condensed matter physics. In MaterialApps LIVE!, HPhi is preinstalled, so you can try out HPhi without the installation process.
The version of “MateriApps LIVE!” I used is ver. 2.3.

2. How to use

Several input files are available in the directory “/usr/share/hphi/samples/“. Here I explain how to calculate the ground state of the Hubbard model by using CG method as an example of HPhi.

Prepare inputs and Run HPhi:

First, launch LXTerminal from System tools, copy the sample directory under the HOME directory, and move into it.

$ cp -r /usr/share/hphi/samples/CG/Hubbard ./ 
$ cd Hubbard

The input “stan.in” exists in the sample directory “Hubbard”.

stan.in

model = "Hubbard"
method = "CG"
lattice = "square"
a0W = 2
a0L = 2
a1W = -2
a1L = 2
t = 1.0
U = 8.0
nelec = 8
2Sz = 0
exct = 1

This input shows that I will obtain the ground state (exct=1) of the Hubbard model at half filling (nelec=8) on the “square” lattice defined by the translational vectors (it{vec{a_0} })=(a0W,a0L), (it{vec{a_1}})=(a1W,a1L) by using CG method. If you want to obtain low excited states, enter the number of excited states in exct.

By executing the following command,  the HPhi simulation is performed.

$ HPhi -s stan.in

This process will finish in about a few seconds.

 

Results:

The output of the calculation is placed in the directory “output”.
For example,  energies of eigenstates up to the “exct” defined in “stan.in” are written in “zvo_energy.dat”.

output/zvo_energy.dat

State 0
Energy -3.7839808089121174
Doublon 0.2912225132545033
Sz 0.0000000000000000

Now exct=1, so this result corresponds to physical quantities of the ground states.

Equal-time Green’s functions are available in “zvo_cisajs_eigen0.dat” and “zvo_cisajscktalt_eigen0.dat”. These quantities are represented in real space, so if you want to see the momentum distribution or structure factors, you need to convert them to those in wave number space by using the Fourier transformation.

To obtain wave-number dependence of physical quantities, I used the tool “greenr2k”, which is also provided in “HPhi” repository. You can copy it from “/usr/share/hphi/tool” on MateriApps LIVE!.

$ cp /usr/share/hphi/tool/greenr2k ./

After copying “greenr2k”, and run the following command2:

$ echo -e "4 2\n G 0 0 0\n X 0.5 0 0\n M 0.5 0.5 0\n G 0 0 0\n 16 16 1" >> geometry.dat
$ ./greenr2k namelist.def geometry.dat

The Fourier transformed results are output to output/zvo_corr_eigen0.dat.

Finally execute the following commands

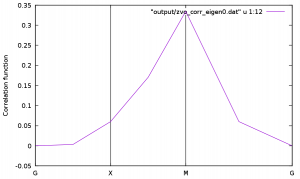
$ gnuplot
  > load "kpath.gp"
  > p "output/zvo_corr_eigen0.dat" u 1:12 w l

and then you will obtain the following figure where the spin structure factor is plotted. The peak of the spin structure factor is located at M=(π, π), which indicates that the antiferromagnetic correlation is well developed in the ground state of the Hubbard model at half filling.