Creating a surface slab model using VESTA
Last Update:2024/12/10
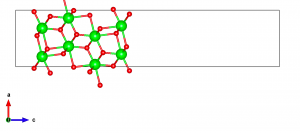
Most first-principles codes rely on the use of the periodic boundary condition. This goes well with bulk crystalline systems, but there are cases where one would want to simulate surface systems for, e.g., heterogeneous catalysis. The usual way to go is to prepare a “slab” model as shown below.
Here, I will walk through using VESTA for the purpose of transforming a bulk t-ZrO2 model to a slab model. I also refer the reader to a nice general description on this topic here.
Let me start again with the CIF file downloaded from the Materials Project as described here. It has been reported that the (101) surface is the most stable (Phys. Rev. B 69, 045402 (2004)), so here I will focus on this surface orientation.
After the CIF is loaded, let me first visualize the (101) surface plane. Go to Edit → Lattice Planes, and click “new” in the “Add lattice planes” panel. A pink-colored plane should show up. Next, select three atoms on the (101) plane by holding the “shift” key and double clicking on the atoms. After that, click on “Calculate the best plane for the selected atoms”, and the end result should look like the following. This will be the plane that I will cleave out as the surface slab model.
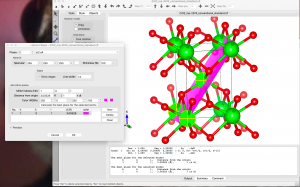
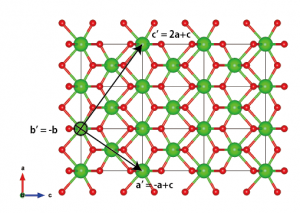
The next step is to rotate the crystal axes so that the new a’ and b’ vectors are in the (101) plane and the new c’ vector points almost perpendicular to the (101) plane. To figure out the new lattice vectors, let’s expand the number of unit cells shown. Go to Objects → Boundary and set x(max), y(max), and z(max) to 3. The unit cell boundaries can be visualized by going to Object → Properties → General, and choosing “All unit cells” in the “Unit cell” panel.
Upon observing the structure, I chose the new lattice vectors to be a‘ = –a+c, b‘ = –b, and c‘ = 2a+c. There are many other possibilities, but make sure to choose a right-handed coordinate system.
Go to Edit→Edit Data→Unit cell, then click on “Remove symmetry“. Next, click on “Transform…”, type in the rotation matrix elements and click Ok:
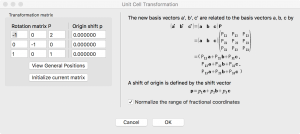
VESTA then asks how to convert the structure, so choose “Search atoms in the new unit-cell…”. Click “Apply” and the result should look something like this:
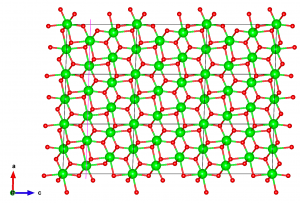
Next, to make some margin for cutting the surface out, I want to extend the supercell in the c direction. Go again to Edit → Edit Data → Transform, click “initialize current matrix“, and set the P33 matrix element to 2.
Now I need to consider where to cleave the surface. The most energetically favorable way to cut the (101) surface has been shown to be in neutral units of (O-Zr-O) layers (Phys. Rev. B 69, 045402 (2004)), so I choose the positions shown in the following figure:
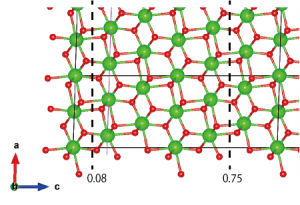
The atoms outside of the region sandwiched by dashed lines need to be removed. Go to Edit → Edit Data → Structure parameters. Click on “z” to order the atoms by their z coordinate in ascending order. Click “OK”, then reopen the Structure parameters window (this redundant step is necessary to avoid a bug that is present in VESTA 3.4.4 Mac OS X version and possibly others). Carefully delete the unnecessary layers (z < 0.08 and z > 0.75).
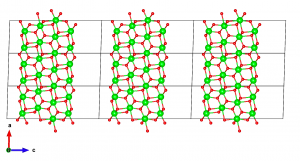
The final step involves introducing a thicker vacuum to avoid cross-talk between adjacent slabs during the simulation. Also, most first-principles codes require the c-axis to be orthogonal to the other axes in order to cancel dipole interactions between adjacent slabs.
I could not find a way to get this done in VESTA. To work around this, I export this data as VASP POSCAR file by going to File → Export Data and choosing VASP as the file type. VESTA asks whether to save the coordinates as fractional coordinates or cartesian coordinates. Be careful to choose cartesian. I open the file in a text editor, and edit the line corresponding to the c vector. In this case, I set c = (0, 0, 30).
Save the POSCAR file, then reopen it in VESTA. The end result should look like this.