To calculate excitation spectrum by exact diagonalization program package HΦ
Last Update:2024/10/10
Introduction
For quantum spin systems, whether the software package can or cannot calculate the dynamical structure factor \(S(q, \omega)\) is an important aspect because \(S(q, \omega)\) is one of the quantities which can be obtained by experiments such as the nuclear scattering. For example, the longitudinal component of the dynamical structure factor \(S_{zz}(q,\omega)\) of the \(S=1/2\) antiferromagnetic Heisenberg chain (AFH chain) is continuous excitation between two modes, \(e_1(q) = J\pi/2 |\sin(q)|\) and \(e_2(q) = J\pi |\sin(q/2)|\) (des Cloizaux-Pearson (dCP) modes). This excitation spectrum can be observed in one-dimensional real materials such as \(\mathrm{Sr}_2\mathrm{Cu}\mathrm{O}_3\).
HΦ(HPhi) is an exact diagonarization solver package for quantum lattice models. HPhi can easily calculate not only the ground state(s) but also excitation spectrum. In this review, we will describe how to calculate \(S(q,\omega)\) of the \(S=1/2\) AFH chain with HPhi.
Use preinstalled HPhi
Since MateriApps LIVE! includes HPhi, users can use HPhi without any process (See another review).
Build from source
Users can get the source code of HPhi from GitHub via git command (in the following, $ in the beginning of a line is a prompt mark).
$ cd && mkdir -p work && cd work $ git clone https://github.com/issp-center-dev/HPhi
Generate Makefile by CMake and build HPhi.
$ mkdir build && cd build $ cmake -DCONFIG=gcc -DCMAKE_INSTALL_PREFIX=../usr ../ $ make -j3 install
Set PATH pointing to $HOME/work/HPhi/usr/bin
$ export PATH=$HOME/work/HPhi/usr/bin:$PATH
Calculate spectrum
Single wave vector
First of all, we should calculate the ground state by HPhi. Prepare the following input file named as gs.in.
method = "cg" model = "spin" lattice = "chain lattice" L = 16 J = 1 2S = 1 2Sz = 0 EigenVecIO = "out"
Invoke HPhi with it to calculate the ground state of 16 sites AFH chain.
$ HPhi -s gs.in
Next, prepare another input file for calculating the excitation spectrum at \(k=\pi\), exc.in.
method = "cg" model = "spin" lattice = "chain lattice" L = 16 J = 1 2S = 1 2Sz = 0 LanczosEPS = 8 CalcSpec = "Normal" SpectrumType = "SzSz" OmegaMin = 0.0 OmegaMax = 3.15 OmegaIM = 0.1 spectrumQL = 0.5
spectrumQL = 0.5 means \(q = 0.5 \times 2\pi = \pi\). Convert it into the input file for the expert mode of HPhi.
HPhi -sdry exc.in
This generates some text files. Then, edit modpara.def and set OmegaOrg (the last of the file) the ground energy (this means the origin of the energy). The ground energy can be found in output/zvo_energy.dat.
$ grep Energy output/zvo_energy.dat Energy -7.1422963606163332
After rewriting modepara.def, execute HPhi to calculate the spectrum.
$ HPhi -e namelist.def
Dynamical Green’s function as a function of the real frequency is written into output/zvo_DynamicalGreen.dat. Excitation spectrum is just the negation of the imaginary part of this. We can see the spectrum by Gnuplot as
$ gnuplot gnuplot> pl 'output/zvo_DynamicalGreen.dat' u 1:(-$4) w l

Sweep in wave vector
HPhi can calculate spectrum only at one wave vector at once. Thus, to obtain the dispersion relation, we should execute the above process many times with changing the wave vector. Since this is very bothering, we prepare the shell script for automation. This script first calculates the ground state and energy, and then calcualtes the excitation spectrum at \(q = 2\pi n/L \,\, (n=0, 1, \dots, L/2)\), and finally writes the result into spectrum-L16.dat.
$ wget http://bit.ly/2GLnsyf -O hphi_AFHchain_spectrum.sh $ sh ./hphi_AFHchain_spectrum.sh
If you want to run this script on MateriApps LIVE!, please rewrite line 44 (gsed command) to “sed -i “s/OmegaOrg[ \t]\+0.0/OmegaOrg $ge/” modpara.def” and install “bc” command by “sudo apt install bc” on the command line before running the above script.
Plot \(S(q,\omega)\) by gnuplot by the following
gnuplot> set dgrid3d 51,51,10 gnuplot> set pm3d map gnuplot> spl 'spectrum-L16.dat' u (2*$1):($2/pi):(-$4) w pm3d
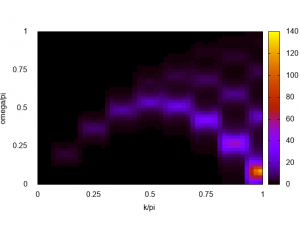
The excitation spectrum of the AFH chain is obtained! The lower dCP mode is clearly seen, especially. When the system is getting larger and larger, the obtained spectrum gets clearer and clearer. The next figure shows the spectrum of \(L=28\) AFH chain obtained by HPhi on the ISSP supercomputer system B (sekirei).
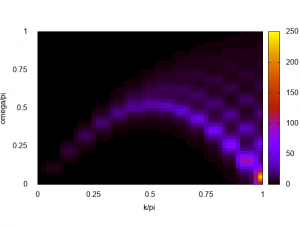
#Revision history
– 2024/10/10: modify a hyperlink

